
【题目】某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图: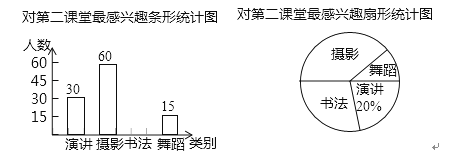
(1)此次调查抽取的学生人数m= 名,其中选择“书法”的学生占抽样人数的百分比n= ;
(2)若该校有3000名学生,请根据以上数据估计该校对“书法”最感兴趣的学生人数.
【答案】
(1)150;30%
(2)
【解答】解:由(1)得:3000×30%=900(名),
答:该校对“书法”最感兴趣的学生人数为900名.
【解析】(1)利用扇形统计图和条形统计图得出参与演讲的人数和所占百分比,进而求出总人数,再求出参加书法的人数,进而求出占抽样人数的百分比;
(2)利用(1)中所求得出该校对“书法”最感兴趣的学生人数.
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.


科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋时期杰出的数学家杨辉是钱塘人,如图是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律. 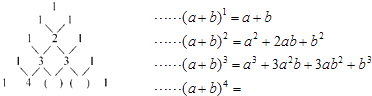
(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过814天是星期 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
最关注的话题 | 街头随访/人 | 网络调查/人 | 合计/人 |
雾霾是什么 | 120 | 200 | |
雾霾治理 | 40%a | 60%a | a |
雾霾中自我防护策略 | 600 | ||
其他话题 | 60 |
(1)参加本次街头随访和网络调查的总人数是多少人,a的值为多少;
(2)请你将以上表格中空白处补充完整;
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是 多少? ;
查看答案和解析>>
科目:初中数学 来源: 题型:
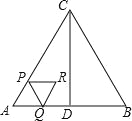
【题目】如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD﹣DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
(1)当点Q在线段AD上时,用含t的代数式表示QR的长;
(2)求点R运动的路程长;
(3)当点Q在线段AD上时,求S与t之间的函数关系式;
(4)直接写出以点B、Q、R为顶点的三角形是直角三角形时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com