
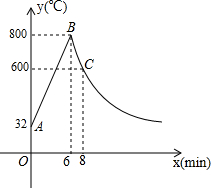
 如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.
如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.分析 (1)待定系数法分别求解可得;
(2)将y=480代入y=$\frac{4800}{x}$,求得x的值即可得出答案.
解答 解:(1)材料煅烧时,设y=kx+32,
当x=6时,y=800,
∴800=6k+32,
∴k=128,
∴材料煅烧时,y=128x+32,
材料锻造时,设y=$\frac{m}{x}$,
当x=8时,y=600,
∴600=$\frac{m}{8}$,
∴m=4800,
∴材料锻造时y=$\frac{4800}{x}$;
(2)把y=480代入y=$\frac{4800}{x}$,得x=10,
∴锻造的时间为:10-6=4(min),
答:锻造的操作时间为4分钟.
点评 本题主要考查反比例函数与一次函数的应用,熟练掌握待定系数法求函数解析式是解题的关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件“任意一个x(x为实数)值,x2是不确定事件” | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投十次一定投中6次 | |
| C. | 为了了解我市各超市销售的速冻食品质量情况,适合采取普查的方式调查 | |
| D. | 投掷一枚质地均匀的硬币10次,可能有5次正面向上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
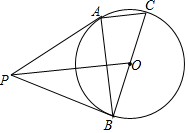 如图,P为⊙O外一点,BC是⊙O的直径,CA为⊙O的一条弦,连接PA、PB,∠PBA=∠C.
如图,P为⊙O外一点,BC是⊙O的直径,CA为⊙O的一条弦,连接PA、PB,∠PBA=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
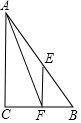 如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )
如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )| A. | △ABC是直角三角形 | B. | AF是△ABC的中位线 | ||
| C. | EF是△ABC的中位线 | D. | △BEF的周长为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com