
 如图,在Rt△ABC中,∠C=90°,CD⊥AB,S△BCD=3S△CAD,则AC﹕BC的值为$\frac{\sqrt{3}}{3}$.
如图,在Rt△ABC中,∠C=90°,CD⊥AB,S△BCD=3S△CAD,则AC﹕BC的值为$\frac{\sqrt{3}}{3}$. 分析 根据条件证得:∠ADC=∠CDB,∠ACD=∠B,得到△BCD∽△CAD,再由相似三角形面积的比等于相似的平方,即可求解.
解答 解:∵S△BCD=3S△CAD,
∴$\frac{{S}_{△CAD}}{{S}_{△BCD}}=\frac{1}{3}$,
∵∠ADC=∠CDB=90°,∠C=90°,
∴∠ACD=∠B=90°-∠A,
∴△BCD∽△CAD,
$(\frac{AC}{BC})^{2}$=$\frac{{S}_{△CAD}}{{S}_{△BCD}}$=$\frac{1}{3}$,
∴$\frac{AC}{BC}=\sqrt{\frac{1}{3}}=\frac{\sqrt{3}}{3}$.
故答案为$\frac{\sqrt{3}}{3}$.
点评 本题主要考查了相似三角形的判定:有两角对应相等的三角形相似,相似三角形的性质:相似三角形的性质:面积之比等于相似比的平方,熟记定理是解决问题的关键.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 有一个角是100°的两个等腰三角形相似 | |
| B. | 全等三角形都是相似三角形 | |
| C. | 两边对应成比例,且有一个角相等的两个三角形相似 | |
| D. | 两条直角边对应成比例的两个直角三角形相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
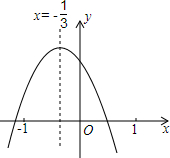 小明从如图所示的二次函数y=ax2+bx+c(a≠0)图象中,观察得出了下面四条信息:①a=$\frac{3}{2}$b;②b2-4ac=0;③ab>0;④a+b+c<0;
小明从如图所示的二次函数y=ax2+bx+c(a≠0)图象中,观察得出了下面四条信息:①a=$\frac{3}{2}$b;②b2-4ac=0;③ab>0;④a+b+c<0;| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com