
【题目】如图,BD 是菱形ABCD 的对角线,∠A=30°.
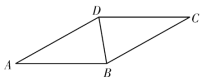
(1)请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,求∠DBF 的度数.
【答案】(1)见解析;(2)45°
【解析】
(1)分别以A、B为圆心,大于![]() 长度为半径画弧,交于线段AB两侧,连接两个交点的直线即为所求;
长度为半径画弧,交于线段AB两侧,连接两个交点的直线即为所求;
(2)根据菱形的性质可以求出∠ABD的度数,再根据FA=FB可得出∠A=∠FBA=30°,再用∠ABD![]() ,即可得出∠DBF的度数.
,即可得出∠DBF的度数.
解:(1)如图所示,直线EF 即为所求;
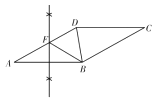
(2)∵四边形ABCD 是菱形,
∴∠ABD=∠DBC, DA∥CB,
∴∠ABC+∠A=180°.
∵∠A=30°,
∴∠ABC=150°.
∴∠ABD=∠DBC=75°
∵EF 垂直平分线段AB,
∴AF=FB.
∴∠A=∠FBA=30°.
∴∠DBF=∠ABD-∠FBA=75°-30°=45°.
故答案为(1)见解析;(2)45°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
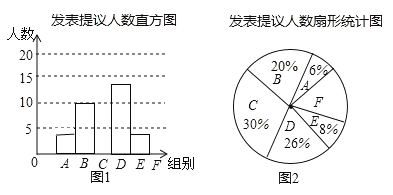
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且点P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点P是线段MN关于点O的关联点.图1是点P为线段MN关于点O的关联点的示意图.
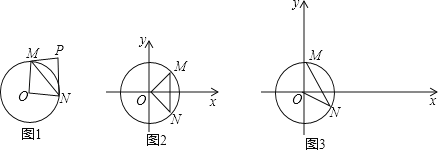
在平面直角坐标系xOy中,⊙O的半径为1.
(1)如图2,已知M(![]() ,
,![]() ),N(
),N(![]() ,﹣
,﹣![]() ),在A(1,0),B(1,1),C(
),在A(1,0),B(1,1),C(![]() ,0)三点中,是线段MN关于点O的关联点的是 ;
,0)三点中,是线段MN关于点O的关联点的是 ;
(2)如图3,M(0,1),N(![]() ,﹣
,﹣![]() ),点D是线段MN关于点O的关联点.
),点D是线段MN关于点O的关联点.
①∠MDN的大小为 ;
②在第一象限内有一点E(![]() m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
③点F在直线y=﹣![]() x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
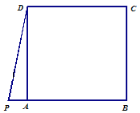
【题目】如图,正方形 ABCD 中,P 是 BA 延长线上一点,且PDA (0 45).点 A,点 E 关于 DP 对称,连接 ED,EP ,并延长 EP 交射线CB 于点 F ,连接 DF .
(1)请按照题目要求补全图形.
(2)求证:∠EDF=∠CDF
(3)求∠EDF(含有 的式子表示);
(4)过 P 做PH⊥DP交 DF 于点 H ,连接 BH , 猜想 AP 与 BH 的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
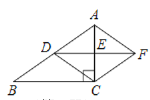
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别为AB,AC的中点,连接DE,将△ADE绕点E旋转180°,得到△CFE,连接AF,CD.
(1)四边形ADCF是什么特殊的四边形?说明理由;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
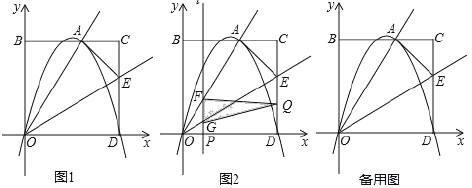
【题目】如图1,矩形OBCD的边OD,OB分别在x轴和y轴上,且B (0,8),D(10,0).点E是DC边上一点,将矩形OBCD沿过点O的射线OE折叠,使点D恰好落在BC边上的点A处.
(1)若抛物线y=ax2+bx经过点A,D,求此抛物线的解析式;
(2)若点M是(2)中抛物线对称轴上的一点,是否存在点M,使△AME为等腰三角形?若存在,直接写出点M的坐标;若不存在,说明理由;
(3)如图2,动点P从点O出发沿x轴正方向以每秒1个单位的速度向终点D运动,动点Q从点D出发沿折线D﹣C﹣A以同样的速度运动,两点同时出发,当一点运动到终点时,另一点也随之停止,过动点P作直线1⊥x轴,依次交射线OA,OE于点F,G,设运动时间为t(秒),△QFG的面积为S,求S与t的函数关系式,并直接写出t的取值范围.(t的取值应保证△QFG的存在)
查看答案和解析>>
科目:初中数学 来源: 题型:
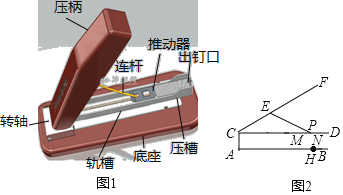
【题目】如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:![]() ≈2.24,
≈2.24,![]() ≈6.08,sin53°≈0.80,cos53°≈0.60)
≈6.08,sin53°≈0.80,cos53°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC.
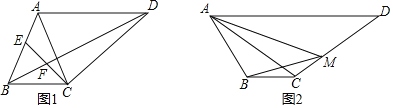
(1)如图1,AB=AC,点E为AB上一点,∠BEC=∠ACD.
①求证:ABBC=ADBE;
②连接BD交CE于F,试探究CF与CE的数量关系,并证明;
(2)如图2,若AB≠AC,点M在CD上,cos∠DAC=cos∠BMA=![]() ,AC=CD=3MC,ADBC=12,直接写出BC的长.
,AC=CD=3MC,ADBC=12,直接写出BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织“校园诗词大会”,全校学生参加初赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了部分学生的成绩(满分100分),整理得到如下不完整的统计图表:
组别 | 成绩x分 | 频数(人数) | 频率 |
第1组 | 50≤x<60 | 6 | 0.12 |
第2组 | 60≤x<70 | 0.16 | |
第3组 | 70≤x<80 | 14 | a |
第4组 | 80≤x<90 | b | |
第5组 | 90≤x<100 | 10 |
请根据图表中所提供的信息回答下列问题:
(1)统计表中a= ,b= ;
(2)请将统计图表补充完整;
(3)根据调查结果,请估计该校1200名学生中,成绩不低于80分的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com