
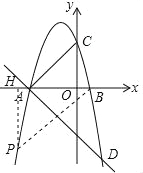
����Ŀ����֪������y=a��x+3����x��1����a��0������x��������������ཻ��A��B���㣬��y���ཻ�ڵ�C��������A��ֱ��y=��![]() x+b�������ߵ���һ������ΪD��
x+b�������ߵ���һ������ΪD��
��1������D�ĺ�����Ϊ2���������ߵĺ�������ʽ��
��2�����ڵ��������ڵ����������е�P��ʹ����A��B��PΪ��������������ABC���ƣ����P�����ꣻ
��3���ڣ�1���������£����E���߶�AD�ϵ�һ�㣨�����˵㣩������BE��һ����Q�ӵ�B���������߶�BE��ÿ��1����λ���ٶ��˶�����E�������߶�ED��ÿ��![]() ����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�

���𰸡�(1) y=��![]() x2��2
x2��2![]() x+3
x+3![]() ��(2) P����������4����
��(2) P������Ϊ����4����![]() ���ͣ���6����
���ͣ���6����![]() ����(3) ��1����4
����(3) ��1����4![]() ��.
��.
��������
�����������1�����ݶ��κ����Ľ���ʽȷ����A��B�����꣬���ֱ�ߵĽ���ʽ�������D�����꣬��������ߵĽ���ʽ����2����PH��x����H�����P������Ϊ��m��n�����֡�BPA�ס�ABC�͡�PBA�ס�ABC���������������ε����ʼ��㼴�ɣ���3����DM��x�ύ��������M����DN��x����N����EF��DM��F���������еĶ������Q���˶�ʱ��t=BE+EFʱ��t��С���ɣ�
�����������1����y=a��x+3����x��1����
���A����������3��0������B����������1��0����
��ֱ��y=��![]() x+b������A��
x+b������A��
��b=��3![]() ��
��
��y=��![]() x��3
x��3![]() ��
��
��x=2ʱ��y=��5![]() ��
��
���D��������2����5![]() ����
����
�ߵ�D���������ϣ�
��a��2+3����2��1��=��5![]() ��
��
��ã�a=��![]() ��
��
�������ߵĽ���ʽΪy=��![]() ��x+3����x��1��=��
��x+3����x��1��=��![]() x2��2
x2��2![]() x+3
x+3![]() ��
��
��2����PH��x����H��
���P��������m��n����
����BPA�ס�ABCʱ����BAC=��PBA��
��tan��BAC=tan��PBA����![]() =
=![]() ��
��
��![]() =
=![]() ����n=��a��m��1����
����n=��a��m��1����
��![]() ��
��
��ã�m1=��4��m2=1���������⣬��ȥ����
��m=��4ʱ��n=5a��
�ߡ�BPA�ס�ABC��
��![]() =
=![]() ����AB2=ACPB��
����AB2=ACPB��
��42=![]()
![]() ��
��
��ã�a1=![]() ���������⣬��ȥ����a2=��
���������⣬��ȥ����a2=��![]() ��
��
��n=5a=��![]() ��
��
���P����������4����![]() ����
����
����PBA�ס�ABCʱ����CBA=��PBA��
��tan��CBA=tan��PBA����![]() =
=![]() ��
��
��![]() =
=![]() ����n=��3a��m��1����
����n=��3a��m��1����
��![]() ��
��
��ã�m1=��6��m2=1���������⣬��ȥ����
��m=��6ʱ��n=21a��
�ߡ�PBA�ס�ABC��
��![]() =
=![]() ����AB2=BCPB��
����AB2=BCPB��
��42=![]()
![]() ��
��
��ã�a1=![]() ���������⣬��ȥ����a2=��
���������⣬��ȥ����a2=��![]() ��
��
���P����������6����![]() ����
����
�������������������ĵ�P������Ϊ����4����![]() ���ͣ���6����
���ͣ���6����![]() ����
����
��3����DM��x�ύ��������M����DN��x����N����EF��DM��F��
��tan��DAN=![]() =
=![]() =
=![]() ��
��
���DAN=60�㣬
���EDF=60�㣬
��DE=![]() =
=![]() EF��
EF��
��Q���˶�ʱ��t=![]() +
+![]() =BE+EF��
=BE+EF��
�൱BE��EF����ʱ��t��С��
��BE��DM��E(1,��4![]() )��
)��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij·�����������վ�������ξ���A��B��Cվ�����յ�վ����վ�ϡ��³˿��������±���ʾ(���ϳ�����Ϊ�����³�����Ϊ��)��
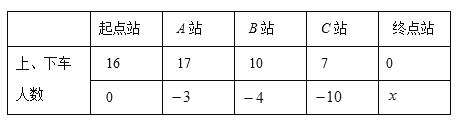
(1)������![]() ��ֵ�� ��
��ֵ�� ��
(2)���˹���������һƱ�ƣ���ÿλ�ϳ��˿�������վ�³�����Ʊ����2Ԫ���ʸó���γ������������Ԫ������ʽ���㣮
(3)ͨ����ʽ���㣬��������ʻ������վ֮��ʱ���ϵij˿���ࣿ���˿������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ѧ��ȤС��Ϊ�˽ⱾУѧ���Ե��ӽ�Ŀ��ϲ���������������˲���ѧ����ϲ����һ���Ŀ���������ѧ��ֻѡһ�ಢ��û�в�ѡ��ģ��������������Ƴ������µ�����ͳ��ͼ�������������������ͼ�����ṩ����Ϣ������������⣺
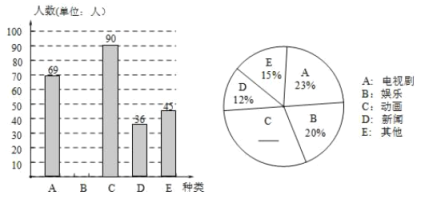
��1�����ε����ѧ������Ϊ__________�����ֽ�Ŀ������ͳ��ͼ����ռԲ�ĽǵĶ�����__________�ȣ�
��2���뽫����ͳ��ͼ����������
��3��������ѧ��2000��ѧ��������Ƹ�Уϲ��������Ŀ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼl��ʾ�������߶�MN���䴹ֱƽ������һ��P�����Ե�PΪԲ�ģ�PMΪ�뾶���Ż������Բ����MN�ϴ��������������Ϊһ���ȱ������εĶ��㣬��Ƶ�PΪ�߶�MN�ġ�����㡱���ر�ģ��������ĵȱ�������ֻ����һ������Ƶ�PΪ�߶�MN�ġ�ǿ����㡱��
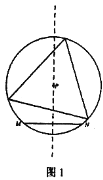
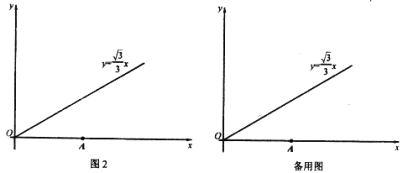
���⣺��ͼ2��ʾ��ƽ��ֱ������ϵxOy�У���A������Ϊ��2![]() ��0������B������y=
��0������B������y=![]() x��x��0���ϡ�
x��x��0���ϡ�
��1���ڵ�C��![]() ��0����D��
��0����D��![]() ��1����E��
��1����E��![]() ��-2���У����Գ�Ϊ�߶�OA�ġ�����㡱����__________.
��-2���У����Գ�Ϊ�߶�OA�ġ�����㡱����__________.
��2������һ�����ڴ���һ��Q�����߶�OA�ġ�����㡱�������߶�OB�ġ�ǿ����㡱�����B�����ꡣ
��3���ڣ�2���������£��Ե�AΪԲ�ģ�ABΪ�뾶��Բ�������Բ��x�ύ�����Ҳ�һ��ΪH��Բ��һ����K��H��������A˳ʱ����ת180���ֹͣ�����K������ת���ĽǶ�Ϊ![]() ��0��<
��0��< ![]() ��180�㣩�����߶�OB��AK�����ڹ���������㡱����ֱ��д��
��180�㣩�����߶�OB��AK�����ڹ���������㡱����ֱ��д��![]() ��ȡֵ��Χ��_______________��
��ȡֵ��Χ��_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ������ͼ��ʾ�������ο������������������ס�±��е����������豻��ס���������У���һ�����ס����С����Ϊa���ڶ������ס����С����Ϊb�����������ס����С����Ϊc��.
��1����һ�����ס������������С����Ϊa,�������ĺ���: ���ڶ������ס������������С����Ϊb,�������ĺ���: �����������ס������������С����Ϊc,�������ĺ���: ��
��2�����������ס�����ĺ�����48�𣿣��ܣ������С����a��b��c��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�CD=6��EΪBC����һ�㣬��EC=2����DEC��DE�۵�����C���ڵ�C'�����۵����A��C'��Eǡ����ͬһֱ���ϣ���AD�ij�Ϊ�� ��
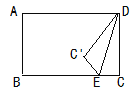
A.8B.9C.![]() D.10
D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������У���ʽ��ȷ����![]() ����
����![]()
A. �˽Ȿ����ѧ��ÿ��ѧϰ���õ�ʱ�䣬����ȫ�����ķ�ʽ
B. Ϊ��֤���ػ���ijɹ����䣬�������е��㲿�����ó�������ķ�ʽ
C. �˽�ij��ÿ��������˿���������ȫ�����ķ�ʽ
D. �˽�ȫ����ѧ����������������ó�������ķ�ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������84 km������ͬʱ����������У��׳����ٶȱ��ҳ����ٶȿ�20 km/h����Сʱ������������
��1�����ҳ����ٶ���ÿСʱ����ǧ�ף�
��2���׳����ٶ���_______ km/h��
��3����������ʱ���׳����ҳ�����ʻ________ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ���ġ��Ļ����š����٣�ijУ��չ�˹�ʫ���ж���������������ȡ����ͬѧ�ijɼ�����ͳ�ƣ������Ƴ����µ�������������ͳ��ͼ������ͼ���ṩ����Ϣ������������⣺
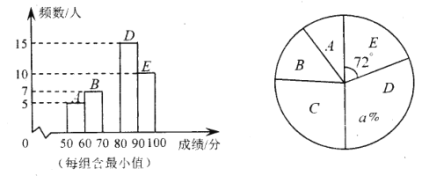
(1)��գ���������Ϊ________��![]() ________��
________��
(2)��Ƶ���ֲ�ֱ��ͼ����������
(3)������![]() ��Բ�ĽǶ�����
��Բ�ĽǶ�����
(4)���ȫУ��2000��ѧ���μ���λ��90������(��90��)Ϊ���㣬��ô���ƻ�����㽱��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com