

|
|


科目:初中数学 来源: 题型:
| 2 |
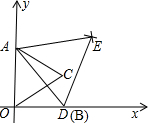
 问:当点E在(不含端点A、B)上运动时,线段MN的长度是否会发生变化?试证明你的结论.
问:当点E在(不含端点A、B)上运动时,线段MN的长度是否会发生变化?试证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |

| 3 |
| 2 |
| 1 |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 于点A,连接OA并延长,与双曲线
于点A,连接OA并延长,与双曲线 交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.
交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.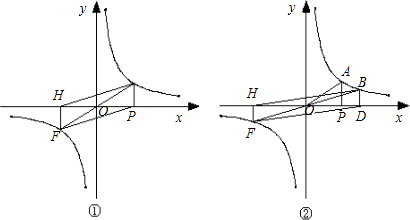
 时,求四边形APFH的面积.
时,求四边形APFH的面积. 交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积.
交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积. ,四边形BDFH的面积为______.(直接写出答案)
,四边形BDFH的面积为______.(直接写出答案)查看答案和解析>>
科目:初中数学 来源:2007年辽宁省大连市甘井子区中考数学模拟试卷(解析版) 题型:解答题
 于点A,连接OA并延长,与双曲线
于点A,连接OA并延长,与双曲线 交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.
交于点F,FH垂直于x轴,垂足为点H,连接AH、PF.
 时,求四边形APFH的面积.
时,求四边形APFH的面积. 交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积.
交于点F,FH垂直于x轴,垂足为点H,连接BH、DF,求四边形BDFH的面积. ,四边形BDFH的面积为______.(直接写出答案)
,四边形BDFH的面积为______.(直接写出答案)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com