
【题目】已知,如图,抛物线与![]() 轴交点坐标为
轴交点坐标为![]() ,
,![]()
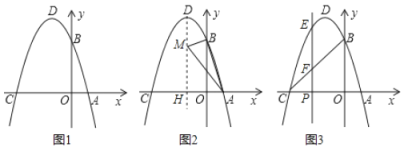
(1)如图1,已知顶点坐标![]() 为
为![]() 或
或![]() 点
点![]() ,选择适当方法求抛物线的解析式;
,选择适当方法求抛物线的解析式;
(2)如图2,在(1)的条件下,在抛物线的对称轴![]() 上求作一点
上求作一点![]() ,使
,使![]() 的周长最小,并求出点
的周长最小,并求出点![]() 的坐标;
的坐标;
(3)如图3,在(1)的条件下,将图2中的对称轴向左移动,交![]() 轴于点
轴于点![]() ,与抛物线,线段
,与抛物线,线段![]() 的交点分别为点
的交点分别为点![]() 、
、![]() ,用含
,用含![]() 的代数式表示线段
的代数式表示线段![]() 的长度,并求出当
的长度,并求出当![]() 为何值时,线段
为何值时,线段![]() 最长.
最长.
【答案】(1)![]() ;(2)点
;(2)点![]() 坐标为
坐标为![]() ;(3)
;(3)![]()
【解析】
(1)根据顶点坐标设顶点式,将点![]() 的坐标代入顶点式解未知系数即得.
的坐标代入顶点式解未知系数即得.
(2)先确定![]() 的周长最小为BC的长度,再用待定系数法求BC的解析式,最后根据M点横坐标确定纵坐标即得.
的周长最小为BC的长度,再用待定系数法求BC的解析式,最后根据M点横坐标确定纵坐标即得.
(3)先用m表示E点和F点的坐标,再利用两点纵坐标之差将线段EF的长度用m表示,最后建立线段EF的长度与m之间的函数关系并将解析式化为顶点式即得.
解:(1)由抛物线的顶点![]() 的坐标
的坐标![]() 可设其解析式为
可设其解析式为![]() ,
,
将点![]() 代入,得:
代入,得:![]() ,
,
解得![]() ,则抛物线解析式为
,则抛物线解析式为![]() ;
;
(2)如图:连接![]() ,交
,交![]() 于点
于点![]()
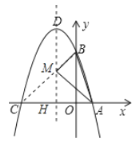
∵A点与C点关于对称轴对称
∴![]()
∵两点之间线段最短
∴![]() 的周长最小为BC的长度
的周长最小为BC的长度
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() ,
,![]() 代入得,
代入得,![]() ,
,
解得:![]()
∴直线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]()
∴点![]() 坐标为
坐标为![]() ;
;
(3)由题意知![]() ,
,![]() ,
,
则![]() ,
,
∴当![]() 时,线段
时,线段![]() 最长.
最长.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a﹣b|=3,|b﹣c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
![]()
A. 在A的左边 B. 介于A、B之间 C. 介于B、C之间 D. 在C的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
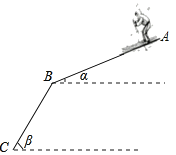
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定不在同一条直线上的点![]() (如图所示),点
(如图所示),点![]() 到点
到点![]() 的距离均等于
的距离均等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() ,
,![]() 的平分线交图形
的平分线交图形![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,延长
,延长![]() 交图形
交图形![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求直线
,求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润![]() (单位:元)与售价
(单位:元)与售价![]() (单位:元/千克)之间的函数关系式.
(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是

A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com