
(本题满分14分,其中第(1)、(2)小题各4分,第(3)小题6分)已知:如图,在平面直角坐标系xOy中,二次函数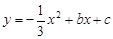 的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
【小题1】(1)求这个二次函数的解析式和它的对称轴;
【小题2】(2)求证:∠ABO=∠CBO;
【小题3】(3)如果点P在直线AB上,且△POB
与△BCD相似,求点P的坐标.
【小题1】(1)解:由题意,得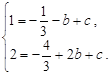 ………………………………………(1分)
………………………………………(1分)
解得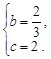 ………………………………………………………………(1分)
………………………………………………………………(1分)
∴所求二次函数的解析式为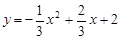 .……………………(1分)
.……………………(1分)
对称轴为直线x=1.
【小题2】(2)证明:由直线OA的表达式y=-x,得点C的坐标为(1,-1).…………(1分)
∵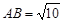 ,
,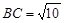 ,∴AB=BC.…………………………………(1分)
,∴AB=BC.…………………………………(1分)
又∵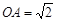 ,
,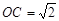 ,∴OA=OC.………………………………(1分)
,∴OA=OC.………………………………(1分)
∴∠ABO=∠CBO.
【小题3】(3)解:由直线OB的表达式y=x,得点D的坐标为(1,1).………………(1分)
由直线AB的表达式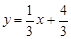 ,
,
得直线与x轴的交点E的坐标为(-4,0).………………………………(1分)
∵△POB与△BCD相似,∠ABO=∠CBO,
∴∠BOP=∠BDC或∠BOP=∠BCD.
(i)当∠BOP=∠BDC时,由∠BDC==135°,得∠BOP=135°.
∴点P不但在直线AB上,而且也在x轴上,即点P与点E重合.
∴点P的坐标为(-4,0).…………………………………………………(2分)
(ii)当∠BOP=∠BCD时,
由△POB∽△BCD,得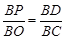 .
.
而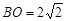 ,
,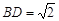 ,
,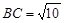 ,∴
,∴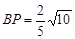 .
.
又∵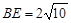 ,∴
,∴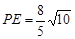 .
.
作PH⊥x轴,垂足为点H,BF⊥x轴,垂足为点F.
∵PH∥BF,∴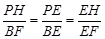 .
.
而BF=2,EF=6,∴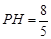 ,
,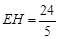 .
.
∴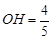 .
.
∴点P的坐标为(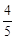 ,
,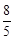 ).………………………………………………(2分)
).………………………………………………(2分)
综上所述,点P的坐标为(-4,0)或(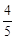 ,
,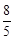 )
)
解析


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
(本题满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角![]() (
(![]() 且
且![]() ≠ 90°),得到Rt△
≠ 90°),得到Rt△![]() ,
,
(1)如图9,当![]() 边经过点B时,求旋转角
边经过点B时,求旋转角![]() 的度数;
的度数;
(2)在三角板旋转的过程中,边![]() 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交![]() 边于点E,联结BE.
边于点E,联结BE.
①当![]() 时,设
时,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当![]() 时,求
时,求![]() 的长.
的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
 (
( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
, 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数; 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交 边于点E,联结BE.
边于点E,联结BE. 时,设
时,设 ,
, ,求
,求 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域; 时,求
时,求 的长.
的长. 

查看答案和解析>>
科目:初中数学 来源:2011届上海市普陀区4月中考模拟数学试卷 题型:解答题
(本题 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角 (
( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
,
(1)如图9,当 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交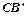 边于点E,联结BE.
边于点E,联结BE.
①当 时,设
时,设 ,
,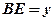 ,求
,求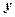 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当 时,求
时,求 的长.
的长. 

查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市考模拟数学试卷 题型:解答题
(本题满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角 (
( 且
且 ≠ 90°),得到Rt△
≠ 90°),得到Rt△ ,
,
(1)如图9,当 边经过点B时,求旋转角
边经过点B时,求旋转角 的度数;
的度数;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 交
交 边于点E,联结BE.
边于点E,联结BE.
①当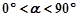 时,设
时,设 ,
, ,求
,求 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域;
②当 时,求
时,求 的长.
的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com