
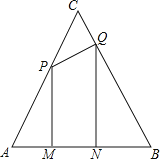
ЁОЬтФПЁПШчЭМЃЌЕШБпШ§НЧаЮABCЕФБпГЄЮЊ8cmЃЌЖЏЕуPДгЕуAГіЗЂвд![]() УыЕФЫйЖШбиACЗНЯђЯђжеЕуCдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂвд
УыЕФЫйЖШбиACЗНЯђЯђжеЕуCдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂвд![]() УыЕФЫйЖШбиCBЗНЯђЯђжеЕуBдЫЖЏЃЌЙ§ЕуPЁЂQЗжБ№зїБпABЕФДЙЯпЖЮPMЁЂQNЃЌДЙзуЗжБ№ЮЊЕуMЁЂ
УыЕФЫйЖШбиCBЗНЯђЯђжеЕуBдЫЖЏЃЌЙ§ЕуPЁЂQЗжБ№зїБпABЕФДЙЯпЖЮPMЁЂQNЃЌДЙзуЗжБ№ЮЊЕуMЁЂ![]() ЩшPЁЂQСНЕудЫЖЏЪБМфЮЊtУы
ЩшPЁЂQСНЕудЫЖЏЪБМфЮЊtУы![]() ЃЌЫФБпаЮMNQPЕФУцЛ§ЮЊ
ЃЌЫФБпаЮMNQPЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ
![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЮЊЕШБпШ§НЧаЮЃП
ЮЊЕШБпШ§НЧаЮЃП
![]() ЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮMNQPЕФУцЛ§SЕШгк
ЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮMNQPЕФУцЛ§SЕШгк![]() ЕФУцЛ§ЕФ
ЕФУцЛ§ЕФ![]() ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
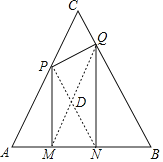
![]() СЌНгPNЁЂQMНЛгкЕуDЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙ
СЌНгPNЁЂQMНЛгкЕуDЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙ![]() ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊЕШБпШ§НЧаЮЃЛЃЈ2ЃЉ
ЮЊЕШБпШ§НЧаЮЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
![]() гЩЬтвтЕУЃК
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌМДЃК
ЪБЃЌМДЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() МДПЩЧѓНтЃЛ
МДПЩЧѓНтЃЛ
![]() гЩЬтвтЕУЃК
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌдк
ЃЌдк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌАДее
ЃЌАДее![]() МДПЩЧѓНтЃЛ
МДПЩЧѓНтЃЛ
![]() ШчЯТЭМЃК
ШчЯТЭМЃК![]() ЃЌАДее
ЃЌАДее![]() ЃЌМДПЩЧѓНтЃЎ
ЃЌМДПЩЧѓНтЃЎ
![]() гЩЬтвтЕУЃК
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌМДЃК
ЪБЃЌМДЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
МДЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊЕШБпШ§НЧаЮЃЛ
ЮЊЕШБпШ§НЧаЮЃЛ
![]() гЩЬтвтЕУЃК
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЩсШЅИКжЕ
ЩсШЅИКжЕ![]() ЃЌ
ЃЌ
ЙЪЃК![]() ЃЛ
ЃЛ
![]() ШчЯТЭМЃК
ШчЯТЭМЃК
![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МДЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ


 ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ
аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЯТСаНсТлЃКЃЈ1ЃЉsinAЃМ1ЃЛЃЈ2ЃЉШєAЃО60ЁуЃЌдђcosAЃО![]() ЃЛЃЈ3ЃЉШєAЃО45ЁуЃЌдђsinAЃОcosAЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
ЃЛЃЈ3ЃЉШєAЃО45ЁуЃЌдђsinAЃОcosAЃЎЦфжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
A. 0Иі B. 1Иі C. 2Иі D. 3Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЁїBPCЪЧЕШБпШ§НЧаЮЃЌBPЁЂCPЕФбгГЄЯпЗжБ№НЛADгкЕуEЁЂFЃЌСЌНсBDЁЂDPЃЌBDгыCFЯрНЛгкЕуHЃЎИјГіЯТСаНсТлЃК
ЂйЁїBDEЁзЁїDPEЃЛЂк![]() =
=![]() ЃЛЂлDP2=PHPBЃЛЂмtanЁЯDBE=2Љ
ЃЛЂлDP2=PHPBЃЛЂмtanЁЯDBE=2Љ![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФЪЧЃЈ ЃЉ
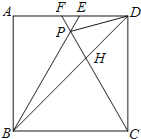
AЃЎЂйЂкЂлЂм BЃЎЂйЂкЂм CЃЎЂкЂлЂм DЃЎЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮOABCЕФЖЅЕуAдкyжсе§АыжсЩЯЃЌЖЅЕуCдкxжсе§АыжсЩЯЃЌХзЮяЯп![]() ЃЈa<0ЃЉЕФЖЅЕуЮЊDЃЌЧвОЙ§ЕуAЁЂBЃЎШєЁїABDЮЊЕШбќжБНЧШ§НЧаЮЃЌдђaЕФжЕЮЊ___________ЃЎ
ЃЈa<0ЃЉЕФЖЅЕуЮЊDЃЌЧвОЙ§ЕуAЁЂBЃЎШєЁїABDЮЊЕШбќжБНЧШ§НЧаЮЃЌдђaЕФжЕЮЊ___________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкПЮЬУЩЯЃЌРЯЪІНЋГ§беЩЋЭтЖМЯрЭЌЕФ1ИіКкЧђКЭШєИЩИіАзЧђЗХШывЛИіВЛЭИУїЕФПкДќВЂНСдШЃЌШУШЋАрЭЌбЇвРДЮНјааУўЧђЪдбщЃЌУПДЮЫцЛњУўГівЛИіЧђЃЌМЧЯТбеЩЋдйЗХЛиНСдШЃЌЯТБэЪЧЪдбщЕУЕНЕФвЛзщЪ§ОнЃЎ
УўЧђЕФДЮЪ§n | 100 | 150 | 200 | 500 | 800 |
УўЕНКкЧђЕФДЮЪ§m | 26 | 37 | 49 | 124 | 200 |
УўЕНКкЧђЕФЦЕТЪ |
|
|
|
| a |
![]() БэжаaЕФжЕЕШгк______ЃЛ
БэжаaЕФжЕЕШгк______ЃЛ
![]() ЙРЫуПкДќжаАзЧђЕФИіЪ§ЃЛ
ЙРЫуПкДќжаАзЧђЕФИіЪ§ЃЛ
![]() гУЛЪїзДЭМЛђСаБэЕФЗНЗЈМЦЫуСЌајСНУћЭЌбЇЖМУўГіАзЧђЕФИХТЪЃЎ
гУЛЪїзДЭМЛђСаБэЕФЗНЗЈМЦЫуСЌајСНУћЭЌбЇЖМУўГіАзЧђЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГЫЎПтЩЯгЮгавЛЕЅПзХзЮяЯпаЭЙАЧХЃЌЫќЕФПчЖШABЮЊ100УзЃЎзюЕЭЫЎЮЛЃЈгыABдкЭЌвЛЦНУцЃЉЪБЧХУцCDОрРыЫЎУц25УзЃЌЧХЙАСНЖЫгаСНИљ25УзИпЕФЫЎФржљBCКЭADЃЌжаМфЕШОрРыЪњСЂ9ИљИжжљжЇГХЧХУцЃЌЙАЖЅе§ЩЯЗНЕФИжжљEFГЄ5УзЃЎ
ЃЈ1ЃЉНЈСЂЪЪЕБЕФжБНЧзјБъЯЕЃЌЧѓХзЮяЯпаЭЧХЙАЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкзюЕЭЫЎЮЛЪБЃЌФмВЂХХЭЈЙ§СНЫвПэ28УзЃЌИп16УзЕФгЮТжТ№ЃПЃЈМйЩшСНгЮТжжЎМфЕФАВШЋМфОрЮЊ4УзЃЉ
ЃЈ3ЃЉгЩгкЯТгЮЫЎПтаюЫЎМАгъМОгАЯьЕМжТЫЎЮЛЩЯеЧЃЌЫЎЮЛзюИпЪББШзюЕЭЫЎЮЛИпГі13УзЃЌЧыЮЪзюИпЫЎЮЛЪБУЛдкЫЎУцвдЯТЕФИжжљзмГЄЮЊЖрЩйУзЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЕуDЁЂEЁЂFЗжБ№дкBCЁЂABЁЂCAЩЯЃЌЧвDEЁЮCAЃЌDFЁЮBAЃЌдђЯТСаШ§жжЫЕЗЈЃК
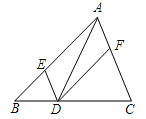
ЃЈ1ЃЉШчЙћЁЯBAC=90ЁуЃЌФЧУДЫФБпаЮAEDFЪЧОиаЮ
ЃЈ2ЃЉШчЙћADЦНЗжЁЯBACЃЌФЧУДЫФБпаЮAEDFЪЧСтаЮ
ЃЈ3ЃЉШчЙћADЁЭBCЧвAB=ACЃЌФЧУДЫФБпаЮAEDFЪЧе§ЗНаЮ ЃЎЦфжае§ШЗЕФга ЃЈ ЃЉ
AЃЎ3Иі BЃЎ2Иі CЃЎ1Иі DЃЎ0Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌвбжЊОЙ§Еу
ЃЌвбжЊОЙ§Еу![]() ЕФжБЯпЕФБэДяЪНЮЊ
ЕФжБЯпЕФБэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНМАЦфЖЅЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕуЃЌЦфжа
ЩЯЕФвЛИіЖЏЕуЃЌЦфжа![]() ЃЌзїжБЯп
ЃЌзїжБЯп![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гк
гк![]() ЃЌНЛХзЮяЯпгк
ЃЌНЛХзЮяЯпгк![]() ЃЌзї
ЃЌзї![]() ЁЮ
ЁЮ![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЮЊОиаЮЃЎЩшОиаЮ
ЮЊОиаЮЃЎЩшОиаЮ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌаДГі
ЃЌаДГі![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓ
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓ![]() ЮЊКЮжЕЪБжмГЄ
ЮЊКЮжЕЪБжмГЄ![]() зюДѓЃЛ
зюДѓЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЙЙГЩЕФШ§НЧаЮЪЧвд
ЙЙГЩЕФШ§НЧаЮЪЧвд![]() ЮЊбќЕФЕШбќШ§НЧаЮЃЎШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу
ЮЊбќЕФЕШбќШ§НЧаЮЃЎШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
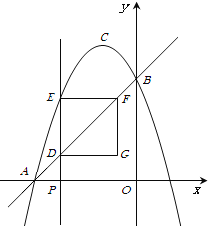
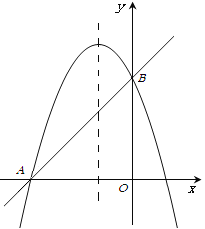
ЭМЂй ЭМЂк
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФПкДќРягаЗжБ№БъзЂ2ЁЂ4ЁЂ6ЕФ3ИіаЁЧђЃЈаЁЧђГ§Ъ§зжВЛЭЌЭтЃЌЦфгрЖМЯрЭЌЃЉЃЌСэга3еХБГУцЭъШЋвЛбљЁЂе§УцЗжБ№аДгаЪ§зж6ЁЂ7ЁЂ8ЕФПЈЦЌЃЎЯжДгПкДќжаШЮвтУўГівЛИіаЁЧђЃЌдйДгет3еХБГУцГЏЩЯЕФПЈЦЌжаШЮвтУўГівЛеХПЈЦЌЃЎ
ЃЈ1ЃЉЧыФугУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌБэЪОГіЫљгаПЩФмГіЯжЕФНсЙћЃЛ
ЃЈ2ЃЉаЁКьКЭаЁРђзігЮЯЗЃЌжЦЖЈСЫСНИігЮЯЗЙцдђЃК
Йцдђ1ЃКШєСНДЮУўГіЕФЪ§зжЃЌжСЩйгавЛДЮЪЧЁА6ЁБЃЌаЁКьгЎЃЛЗёдђЃЌаЁРђгЎЃЎ
Йцдђ2ЃКШєУўГіЕФПЈЦЌЩЯЕФЪ§зжЪЧЧђЩЯЪ§зжЕФећЪ§БЖЪБЃЌаЁКьгЎЃЛЗёдђЃЌаЁРђгЎЃЎ
аЁКьвЊЯыдкгЮЯЗжаЛёЪЄЃЌЫ§ЛсбЁдёФФвЛжжЙцдђЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com