
【题目】在如图所示的5×5网格中,小方格的边长为1.
(1)图中格点正方形ABCD的面积为________;
(2)若连接AC,则以AC为边的正方形的面积为________;
(3)在所给网格中画一个格点正方形,使其各边都不在格线上且面积最大,你所画的正方形面积为_____.

科目:初中数学 来源: 题型:
【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA’(点A落在直线l上点A’处、线段AP上的所有点与线段PA’上的点对应)如图1
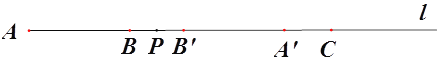
(1)若翻折后A’C=2,则翻折前线段AP= ;
(2)若点P在线段BC上运动,点M为线段A’C的中点,求线段PM的长度;
(3)若点P 在线段BC上运动,点N为B’P的中点,点M为线段A’C的中点,设AP=x,用x表示A’M+PN.

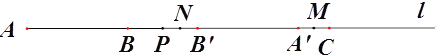
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答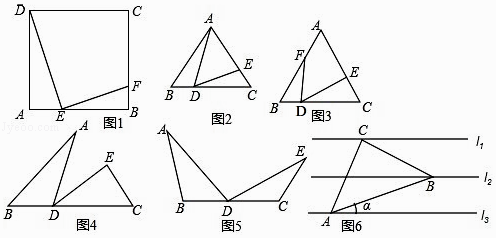
(1)如图1,已知E是矩形ABCD的边AB上一点,EF⊥DE交BC于点F,证明:△ADE∽△BFE.
(2)这个相似的基本图形像字母K,可以称为“K”型相似,但更因为图形的结构特征是一条线上有3个垂直关系,也常被称为“一线三垂直”,那普通的3个等角又会怎样呢?
变式一如图2,已知等边三角形ABC,点D、E分别为BC,AC上的点,∠ADE=60°.
①图中有相似三角形吗?请说明理由.
②如图3,若将∠ADE在△ABC的内部(∠ADE两边不与BC重合),绕点D逆时针旋转一定的角度,还有相似三角形吗?
(3)变式二如图4,隐藏变式1图形中的线段AE,在得到的新图形中.
①如果∠B=∠C=∠ADE=50°,图中有相似三角形吗?请说明理由.
②如图5,若∠B=∠C=∠ADE=∠a,∠a为任意角,还有相似三角形吗?
(4)交式三已知,相邻两条平形直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则cosa的值是(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是王老师在数学课堂上给同学们出的一道数学题,要求对以下实数进行分类填空:
-![]() ,0,
,0,![]() ,
,![]() ,18,
,18,![]() ,
,![]() ,-0.56,3.14159,
,-0.56,3.14159,![]() ,
,![]() ,
,![]() ,0.8080080008…,-
,0.8080080008…,-![]() .
.
(1)有理数集合:________________________________________________________________________;
(2)无理数集合:________________________________________________________________________;
(3)非负整数集合:________________________________________________________________________;
(4)分数集合:________________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考: 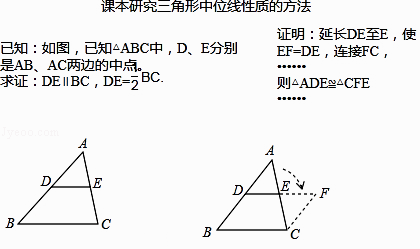 请你利用小亮的发现解决下列问题:
请你利用小亮的发现解决下列问题:
(1)如图1,AD是△ABC的中线,BE交AC于E,交AD于E,且AE=EF,求证:AC=BF. 请你帮助小亮写出辅助线作法并完成论证过程: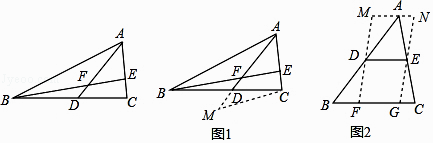
(2)解决问题:如图2,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FE、GE的延长线交于M、N,则四边形MFGN周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题: 
(1)探究:若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是;如图2,当a=°时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=(用含有R、m的代数式表示)
(4)拓展:如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 , 并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
观察:下面这些几何体都是简单几何体,请您仔细观察.
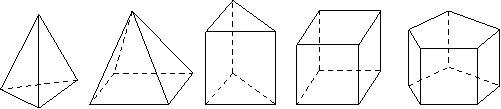
![]()
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体 | a | b | c | d | e |
棱数(E) | 6 | 9 | 15 | ||
面数(F) | 4 | 5 | 5 | 6 | |
顶点数(V) | 4 | 5 | 8 |
发现:(1)简单几何中,![]() ;
;
(2)简单几何中,每条棱都是 个面的公共边;
(3)在正方体中,每个顶点处有 条棱,每条棱都有 个顶点,所以有2![]() 3
3![]() .
.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有 条棱, 个顶点,每个顶点处有 条棱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,点E在BC边上,且CE=2,AE与BD交于点F,连接CF,则下列结论不正确的是( ) 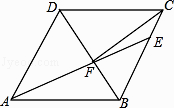
A.△ABF≌△CBF
B.△ADF∽△EBF
C.tan∠EAB= ![]()
D.S△EAB=6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
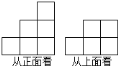
【题目】由若干个(大于![]() 个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com