
【题目】如图,点B、E、F、C在一条直线上,AB=DE=10,AC=DF,BE=CF=CE.
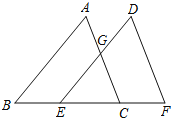
(1)求证:AB∥DE;
(2)求EG的长.
【答案】(1)详见解析;(2)5
【解析】
(1)由BE=CF,利用等式的性质得到BC=EF,利用SSS得到三角形ABC与三角形DEF全等,利用全等三角形对应角相等得到一对同位角相等,利用同位角相等两直线平行即可得证;
(2)由BE=CE得到E为BC中点,再由GE与AB平行,得到GE为中位线,利用中位线定理得到AB=2EG,即可求出EG的长.
解:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
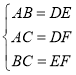 ,
,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE;
(2)∵GE∥AB,E为BC中点,
∴G为AC中点,即GE为△ABC的中位线,
∴EG=![]() AB=5.
AB=5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
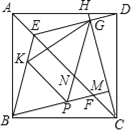
【题目】如图,四边形ABCD为正方形,H是AD上任意一点,连接CH,过B作BM⊥CH于M,交AC于F,过D作DE∥BM交AC于E,交CH于G,在线段BF上作PF=DG,连接PG,BE,其中PG交AC于N点,K为BE上一点,连接PK,KG,若∠BPK=∠GPK,CG=12,KP:EF=3:5,求![]() 的值为__.
的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
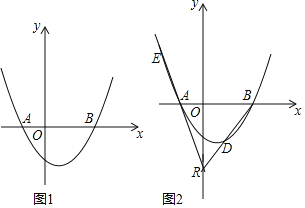
【题目】已知抛物线y=a(x2-cx-2c2)(a>0)交x轴于A、B两点(点A在点B的左侧),交y轴于点C.
(1) 取A(-1,0),则点B的坐标为___________;
(2) 若A(-1,0),a=1,点P为第一象限的抛物线,以P为圆心,![]() 为半径的圆恰好与AC相切,求P点坐标;
为半径的圆恰好与AC相切,求P点坐标;
(3) 如图,点R(0,n)在y轴负半轴上,直线RB交抛物线于另一点D,直线RA交抛物线于E.若DR=DB,EF⊥y轴于F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是网格中的两个格点,点C也是网格中的一个格点,连接AB、BC、AC,当△ABC为等腰三角形时,格点C的不同位置有 处,设网格中的每个小正方形的边长为1,则所有满足题意的等腰三角形ABC的面积之和等于 .
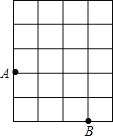
查看答案和解析>>
科目:初中数学 来源: 题型:
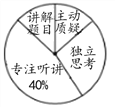
【题目】某地区教育部门为了解初中数学课堂中学生参与情况,并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价.检测小组随机抽查部分学校若干名学生,并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图(均不完整).请根据统计图中的信息解答下列问题:
(1)本次抽查的样本容量是 ;
(2)在扇形统计图中,“主动质疑”对应的圆心角为 度;
(3)将条形统计图补充完整;
(4)如果该地区初中学生共有60000名,那么在课堂中能“独立思考”的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
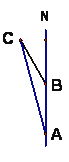
【题目】如图,上午9时,一条渔船从A出发,以12海里/时的速度向正北航行,11时到达B处,从A、B处望小岛C,测得∠NAC=15°,∠NBC=30°.若小岛周围12.3海里内有暗礁,问该渔船继续向正北航行有无触礁危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数![]() 、
、![]() 、
、![]() ,用
,用![]() 表示这三个数的中位数,用
表示这三个数的中位数,用![]() 表示这三个数中最大数,例如:
表示这三个数中最大数,例如:![]() ,
,![]() ,
,![]() .
.
解决问题:
(1)填空:![]() ,如果
,如果![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
(2)如果![]() ,求
,求![]() 的值;
的值;
(3)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
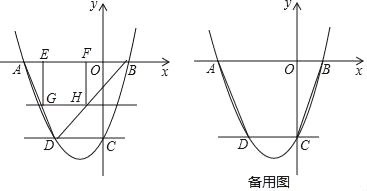
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com