
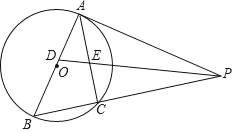
【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,![]()
【解析】(1)易证∠APE=∠BPD,∠EAP=∠B,从而可知△PAE∽△PBD,利用相似三角形的性质即可求出答案.
(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,易求得AE=2,BD=3,由(1)可知:![]() ,从而可知cos∠BDF=cos∠BAC=cos∠APC=
,从而可知cos∠BDF=cos∠BAC=cos∠APC=![]() ,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
(1)∵PD平分∠APB,
∴∠APE=∠BPD,
∵AP与⊙O相切,
∴∠BAP=∠BAC+∠EAP=90°,
∵AB是⊙O的直径,
∴∠ACB=∠BAC+∠B=90°,
∴∠EAP=∠B,
∴△PAE∽△PBD,
∴![]() ,
,
∴PABD=PBAE;
(2)如图,过点D作DF⊥PB于点F,作DG⊥AC于点G,
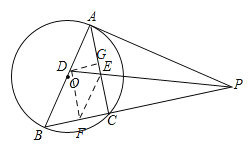
∵PD平分∠APB,AD⊥AP,DF⊥PB,
∴AD=DF,
∵∠EAP=∠B,
∴∠APC=∠BAC,
易证:DF∥AC,
∴∠BDF=∠BAC,
由于AE,BD(AE<BD)的长是x2﹣5x+6=0的两个实数根,
解得:AE=2,BD=3,
∴由(1)可知:![]() ,
,
∴cos∠APC=![]() ,
,
∴cos∠BDF=cos∠APC=![]() ,
,
∴![]() ,
,
∴DF=2,
∴DF=AE,
∴四边形ADFE是平行四边形,
∵AD=DF,
∴四边形ADFE是菱形,此时点F即为M点,
∵cos∠BAC=cos∠APC=![]() ,
,
∴sin∠BAC=![]() ,
,
∴![]() ,
,
∴DG=![]() ,
,
∴菱形ADME的面积为:DGAE=2×![]() =
=![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .设
.设![]() 为最长边.当
为最长边.当![]() 时,
时,![]() 是直角三角形;当
是直角三角形;当![]() 时,利用代数式
时,利用代数式![]() 和
和![]() 的大小关系,探究
的大小关系,探究![]() 的形状(按角分类).
的形状(按角分类).
(1)当![]() 三边分别为6、8、9时,
三边分别为6、8、9时,![]() 为______三角形;当
为______三角形;当![]() 三边分别为6、8、11时,
三边分别为6、8、11时,![]() 为______三角形.
为______三角形.
(2)猜想,当![]() ______
______![]() 时,
时,![]() 为锐角三角形;当
为锐角三角形;当![]() ______
______![]() 时,
时,![]() 为钝角三角形.
为钝角三角形.
(3)判断当![]() ,
,![]() 时,
时,![]() 的形状,并求出对应的
的形状,并求出对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
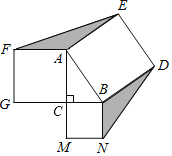
【题目】如图,△ABC中,∠ACB=90°,AC=8,BC=6,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、ND,则图中阴影部分的面积之和等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
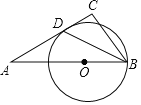
【题目】如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2![]() ,则线段CD的长是( )
,则线段CD的长是( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
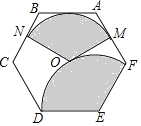
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
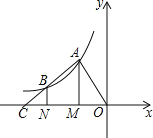
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=2cm,BC=3cm,点P沿B→A→D运动,运动到点D时停止运动,点P运动的同时,另一点Q从B→C运动,速度是点P的一半,当点P停止运动时,点Q也停止运动.设点P运动的路程为xcm,其中设![]() ,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.
,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.
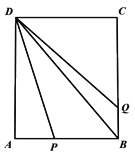
(1)如图是画出的函数![]() 与x的函数图象,观察图象.当x=1时,
与x的函数图象,观察图象.当x=1时,![]() =_____;并写出函数的一条性质:________________________________________.
=_____;并写出函数的一条性质:________________________________________.
(2)请帮助可可写出![]() 与x的函数关系式(不用写出取值范围)__________________.
与x的函数关系式(不用写出取值范围)__________________.
(3)请按照列表、描点、连线的步骤在同一直角坐标系中,画出函数![]() 的图象.
的图象.
(4)结合画出函数图象,解决问题:当![]() 时,点P运动的路程x=_______.
时,点P运动的路程x=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
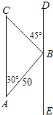
【题目】一架外国侦察机沿![]() 方向侵入我国领空进行非法侦察,我空军的战斗机沿
方向侵入我国领空进行非法侦察,我空军的战斗机沿![]() 方向与外国侦察机平行飞行,进行跟踪监视,我机在
方向与外国侦察机平行飞行,进行跟踪监视,我机在![]() 处与外国侦察机
处与外国侦察机![]() 处的距离为
处的距离为![]() 米,
米,![]() 为
为![]() ,这时外国侦察机突然转向,以偏左
,这时外国侦察机突然转向,以偏左![]() 的方向飞行,我机继续沿
的方向飞行,我机继续沿![]() 方向以
方向以![]() 米/秒的速度飞行,外国侦察机在
米/秒的速度飞行,外国侦察机在![]() 点故意撞击我战斗机,使我战斗机受损.问外国侦察机由
点故意撞击我战斗机,使我战斗机受损.问外国侦察机由![]() 到
到![]() 的速度是多少?(结果保留整数,参考数据
的速度是多少?(结果保留整数,参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com