
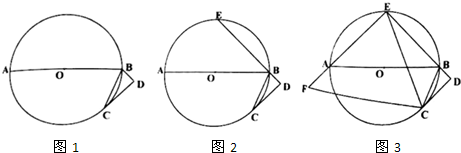
分析 (1)如图1中,欲证明BC平分∠ABD,只要证明∠CBD=∠CBO,只要证明BD∥OC即可.
(2)如图2中,连接AE,连接CO并延长交AE于M欲证明$\widehat{AC}$=$\widehat{EC}$,只要证明CM⊥AE即可.
(3)如图3中,连接AC,连接CO并延长交AE于M,过F作FH⊥CE于H,首先证明△FHE≌△ACB,根据tan∠FCE=$\frac{FH}{CH}$=$\frac{12}{7}$,设FH=12k,CH=7k,列出方程求出k,通过解直角三角形分别求出EF、AE即可解决问题.
解答 (1)证明:如图1中,连接OC,
∵AB是⊙O直径,DC是⊙O切线,
∴OC⊥CD,
∴∠OCD=90°,∵BD⊥CD,∴∠D=90°,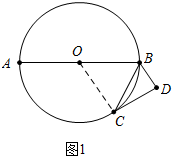
∴∠OCD+∠D=180°,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OB=OC,
∴∠OCB=∠OBC,
∴∠OBC=∠CBD,
∴BC平分∠OBD.
(2)证明:如图2中,连接AE,连接CO并延长交AE于M.
∵AB是直径,
∴∠AEB=90°,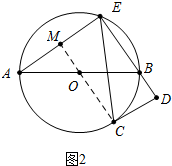
∵CM∥DB,
∴∠AMC=∠AEB=90°,
∴CM⊥AE,
∴∠AMC=∠AEB=90°,
∴CM⊥AE,且CM经过圆心O,
∴$\widehat{AC}$=$\widehat{EC}$.
(3)解:如图3中,连接AC,连接CO并延长交AE于M,过F作FH⊥CE于H, ∵FH⊥CE,
∵FH⊥CE,
∴∠FHE=∠FHC=90°,
由(2)可知∠AMC=90°,
∴∠CME=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠FHE=∠ACB=90°,
∵FH=AB,∠FEH=∠ABC,
∴△FHE≌△ACB,
∴FH=AC,EH=BC,
在RT△FHC中,tan∠FCE=$\frac{FH}{CH}$=$\frac{12}{7}$,设FH=12k,CH=7k,
∴FH=AC=12k,
∵$\widehat{AC}$=$\widehat{EC}$,
∴CE=AC=12k,
∴EH=BC=5k,
∵BC=5,
∴5k=5,
∴k=1,∴AC=12,
在RT△ACB中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,∴AB=EF=13,
在RT△ACB中,sin∠ABC=$\frac{AC}{AB}$=$\frac{12}{13}$,∵∠ABC=∠CBD,
在RT△CBD中,sin∠CBD=$\frac{CD}{BC}$=$\frac{12}{13}$,∴CD=$\frac{60}{13}$,
∵∠AED=∠D=∠ACB=90°,
∴四边形CMED是矩形,
∴CD=ME=$\frac{60}{13}$,
∴AM=ME,
∴AE=2ME=$\frac{120}{13}$,
∴AF=EF-AE=$\frac{49}{13}$.
点评 本题考查圆综合题、切线的性质、垂径定理、勾股定理、三角函数、全等三角形的判定和性质等知识,解题关键是添加辅助线构造全等三角形,灵活运用圆的有关性质解决问题,属于中考常考题型.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{a}$ | B. | a-2 | C. | $\frac{a-2}{a}$ | D. | $\frac{a-4}{{a}^{2}+2a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
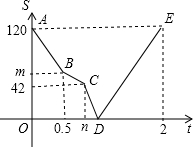 一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th后,与客车的距离为Skm,图中的折线(A→B→C→D→E)表示S与t之间的函数关系.
一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th后,与客车的距离为Skm,图中的折线(A→B→C→D→E)表示S与t之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 至少有1个球是红球 | B. | 至少有1个球是白球 | ||
| C. | 至少有2个球是红球 | D. | 至少有2个球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.946亿元 | B. | 1.946×102亿元 | C. | 1.946×101亿元 | D. | 0.1946×103亿元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 至少有1个球是黑球 | B. | 至少有1个球是白球 | ||
| C. | 至少有2个球是黑球 | D. | 至少有2个球是白球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com