
【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.

(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=![]() ∠E;
∠E;
(3)猜想:若∠En=b°,求∠BEC的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)∠BEC=2nb°.
【解析】试题分析:(1)先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;
(2)先根据∠ABE和∠DCE的平分线交点为E1,运用(1)中的结论,得出∠CE1B=∠ABE1+∠DCE1= ![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=
∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C=![]() ∠BEC;…据此得到规律∠En=
∠BEC;…据此得到规律∠En=![]() ∠BEC,最后求得∠BEC的度数.
∠BEC,最后求得∠BEC的度数.
试题解析:(1)如图①,过E作EF∥AB,
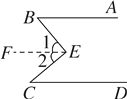
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,
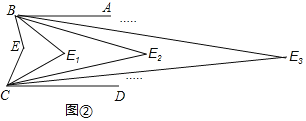
∴由(1)可得,
∠CE1B=∠ABE1+∠DCE1=![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;
∠BEC;
∵∠ABE1和∠DCE1的平分线交点为E2,
∴由(1)可得,
∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)如图2,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=![]() ∠ABE2+
∠ABE2+![]() ∠DCE2=
∠DCE2=![]() ∠CE2B=
∠CE2B=![]() ∠BEC;
∠BEC;
…
以此类推,∠En=![]() ∠BEC,
∠BEC,
∴当∠En=α度时,∠BEC等于2nα度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
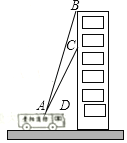
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】18世纪最杰出的瑞士数学家欧拉,最先把关于x的多项式用符号“f(x)”表示,如f(x)=﹣3x2+2x﹣1,把x=﹣2时多项式的值表示为f(﹣2),则f(﹣2)=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过B(﹣1,0),D(﹣2,5)两点,与x轴另一交点为A,点H是线段AB上一动点,过点H的直线PQ⊥x轴,分别交直线AD、抛物线于点Q,P.
经过B(﹣1,0),D(﹣2,5)两点,与x轴另一交点为A,点H是线段AB上一动点,过点H的直线PQ⊥x轴,分别交直线AD、抛物线于点Q,P.
(1)求抛物线的解析式;
(2)是否存在点P,使∠APB=90°,若存在,求出点P的横坐标,若不存在,说明理由;
(3)连接BQ,一动点M从点B出发,沿线段BQ以每秒1个单位的速度运动到Q,再沿线段QD以每秒![]() 个单位的速度运动到D后停止,当点Q的坐标是多少时,点M在整个运动过程中用时t最少?
个单位的速度运动到D后停止,当点Q的坐标是多少时,点M在整个运动过程中用时t最少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块三角板ABC的直角顶点C放在直尺的一边PQ上,直尺的另一边MN与三角板的两边AC、BC分别交于两点E、D,且AD为∠BAC的平分线,∠B=300,∠ADE=150.
(1)求∠BDN的度数;
(2)求证:CD=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:

(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空: a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com