
分析 (1)求方程2x+y=5的正整数解,可给定x一个正整数值,计算y的值,如果y的值也是正整数,那么就是原方程的一组正整数解.
(2)参照例题的解题思路进行解答;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.则根据题意得:3m+5n=35,其中m、n均为自然数.解该二元一次方程即可.
解答 解:
(1)由2x+y=5,得y=5-2x(x、y为正整数).
所以$\left\{\begin{array}{l}{x>0}\\{5-2x>0}\end{array}\right.$,即0<x<$\frac{5}{2}$
∴当x=1时,y=3;
当x=2时,y=1.
即方程的正整数解是$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.(只要写出其中的一组即可)
(2)同样,若$\frac{6}{x-2}$为自然数,
则有:0<x-2≤6,即2<x≤8.
当x=3时,$\frac{6}{x-2}$=6;
当x=4时,$\frac{6}{x-2}$=3;
当x=5时,$\frac{6}{x-2}$=2;
当x=8时,$\frac{6}{x-2}$=1.
即满足条件x的值有4个,
故选C.
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=35,其中m、n均为自然数.
于是有:n=$\frac{35-3m}{5}$,
解得:$\left\{\begin{array}{l}{m>0}\\{7-\frac{3}{5}m>0}\end{array}\right.$,
所以0<m<$\frac{35}{3}$.
由于n=7-$\frac{3}{5}$m为正整数,则$\frac{3}{5}$m为正整数,可知m为5的倍数.
∴当m=5时,n=4;
当m=10时,n=1.
答:有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;
或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
点评 本题考查了二元一次方程的应用,解题关键是要读懂题目给出的已知条件,根据条件求解.注意笔记本和钢笔是整体,所有不可能出现小数和负数,这也就说要求的是正整数.


科目:初中数学 来源: 题型:解答题
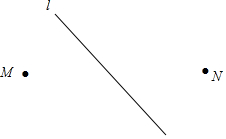 2016年7月31日下午,张家口和北京延庆区同时举办“纪念申冬奥成功一周年活动”,并在该活动上表明,张家口要筹划建成一个以崇礼为核心、周边的赤城、张北等为补充的集中连片滑雪大区,形成能让1000万人同时滑雪的区域.如图,规划人员计划在高速公路l旁的大片空地建设M和N两个滑雪场,同时还要建设两条道路使得滑雪场M和N各自到高速公路l的距离都最近,请你帮规划人员设计出这两条道路.
2016年7月31日下午,张家口和北京延庆区同时举办“纪念申冬奥成功一周年活动”,并在该活动上表明,张家口要筹划建成一个以崇礼为核心、周边的赤城、张北等为补充的集中连片滑雪大区,形成能让1000万人同时滑雪的区域.如图,规划人员计划在高速公路l旁的大片空地建设M和N两个滑雪场,同时还要建设两条道路使得滑雪场M和N各自到高速公路l的距离都最近,请你帮规划人员设计出这两条道路.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | -3 | C. | 12 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
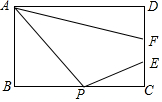 如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com