
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | -4 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 80 | B. | 90 | C. | 60 | D. | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn-1的面积为$\frac{{5}^{n}}{{2}^{2n-1}}$.
如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn-1的面积为$\frac{{5}^{n}}{{2}^{2n-1}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
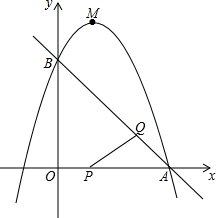 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以$\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以$\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.
如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 唯一有解 | B. | 无穷多解 | C. | 无解 | D. | 都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com