
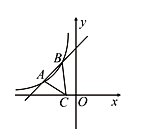
【题目】已知P是⊙O外一点,PO交⊙O于点C,OC=CP=2,弦AB⊥OC,∠AOC的度数为60°,连接PB.
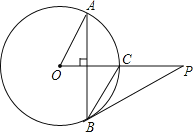
(1)求BC的长;
(2)求证:PB是⊙O的切线.
【答案】(1)BC=2;(2)见解析
【解析】
试题分析:(1)连接OB,根据已知条件判定△OBC的等边三角形,则BC=OC=2;
(2)欲证明PB是⊙O的切线,只需证得OB⊥PB即可.
(1)解:如图,连接OB.
∵AB⊥OC,∠AOC=60°,
∴∠OAB=30°,
∵OB=OA,
∴∠OBA=∠OAB=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC的等边三角形,
∴BC=OC.
又OC=2,
∴BC=2;
(2)证明:由(1)知,△OBC的等边三角形,则∠COB=60°,BC=OC.
∵OC=CP,
∴BC=PC,
∴∠P=∠CBP.
又∵∠OCB=60°,∠OCB=2∠P,
∴∠P=30°,
∴∠OBP=90°,即OB⊥PB.
又∵OB是半径,
∴PB是⊙O的切线.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).
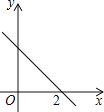
查看答案和解析>>
科目:初中数学 来源: 题型:
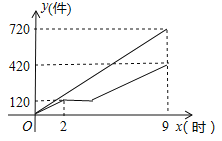
【题目】甲、乙两车间同时开始加工一批服装.从幵始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
(1)甲车间每小时加工服装件数为 件;这批服装的总件数为 件.
(2)求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;
(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭![]() 出发,晚上停留在
出发,晚上停留在![]() 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
+5,-8,+10,-12,+6,-18,+5,-2.
(1)![]() 处在岗亭
处在岗亭![]() 的什么方向?距离岗亭
的什么方向?距离岗亭![]() 多远?
多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有4个小球,分别标有1,2,3,7四个数字,这些小球除所标数字不同外,其余方面完全相同,甲、乙两人每次同时从袋子中各随机摸出一个小球,记下小球上的数字,并计算它们的和.
(1)请用画树状图或列表的方法,求两数和是8的概率;
(2)甲、乙两人想用这种方法做游戏,他们规定:若两数之和是2的倍数时,甲得3分;若两数之和是3的倍数时,乙得2分;当两数之和是其他数值时,两人均不得分.你认为这个游戏公平吗?请说明理由;若你认为不公平,请你修改得分规则,使游戏公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B两点,且AB=8,点A表示的数为6;动点P从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)写出数轴上点B表示的数是 ;
(2)当t=2时,线段PQ的长是 ;
(3)当0<t<3时,则线段AP= ;(用含t的式子表示)
(4)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于A(-3,2),B(n,4)两点.
)的图象交于A(-3,2),B(n,4)两点.
(1)求一次函数与反比例函数的解析式;
(2)点C(-1,0)是![]() 轴上一点,求△ABC的面积.
轴上一点,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y=x+2分别与x轴,y轴交于点M、N,边长为1的正方形OABC的一个顶点O在坐标系原点,直线AN与MC交于点P,若正方形绕点O旋转一周,则点P到点(0,1)长度的最小值是___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com