Question

7．如图①已知抛物线y=ax²+bx+c的对称轴是y轴，求经过点（0，-1）（2，0）
（1）求该抛物线的解析式；
（2）如图②，点P是抛物线上任意一点，过点P作直线l：y=-2的垂线，垂足为Q，求证：PO=PQ；
（3）请你参考（2）中结论解决下列问题
①如图③，过原点任意作直线AB，交抛物线y=ax²+bx+c于点A，B，分别过A，B两点作之下l的垂线，垂足分别是点M，N．连结ON，OM，求证：ON⊥OM；
②如图④，在图中有一点D（1，1），试探究在该抛物线上是否存在点F，使得FD+FO取得最小值？若存在，求出点F的坐标；若不存在，请说明理由．

Answer 1

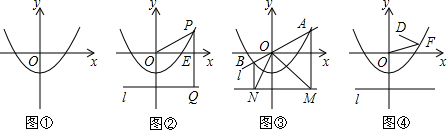
分析 （1）由抛物线y=ax²+bx+c的对称轴是y轴，就可以得出-$\frac{b}{2a}$=0，由待定系数法求可以求出抛物线的解析式；
（2）由（1）设出P的坐标，可得PE和OE的值，从而用勾股定理求出PO的值，和PQ=PE+EQ的值进行对比即得出结论；
（3）①由（2）的结论就可以得出BO=BN，AO=AM，由三角形的内角和定理及平行线的性质就可以求出∠MON=90°而得出结论；
②如图③，作F′H⊥l于H，DF⊥l于G，交抛物线与F，作F′E⊥DG于E，由（2）的结论和根据矩形的性质可以得出结论．

解答 解：（1）由题意，得
$\left\{\begin{array}{l}{-\frac{b}{2a}=0}\\{c=-1}\\{4a+2b+c=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=0}\\{c=-1}\end{array}\right.$，
∴抛物线的解析式为：y=$\frac{1}{4}$x²-1；

（2）如图②，设P（a，$\frac{1}{4}$a²-1），则OE=a，PE=$\frac{1}{4}$a²-1，
∵PQ⊥l，
∴EQ=2，
∴QP=$\frac{1}{4}$a²+1．
在Rt△POE中，由勾股定理，得
PO=$\sqrt{{a}^{2}+（\frac{1}{4}{a}^{2}-1）^{2}}$=$\frac{1}{4}$a²+1，
∴PO=PQ；

（3）①如图③，∵BN⊥l，AM⊥l，
∴BN=BO，AM=AO，BN∥AM，
∴∠BNO=∠BON，∠AOM=∠AMO，∠ABN+∠BAM=180°．
∵∠BNO+∠BON+∠NBO=180°，∠AOM+∠AMO+∠OAM=180°，
∴∠BNO+∠BON+∠NBO+∠AOM+∠AMO+∠OAM=360°
∴2∠BON+2∠AOM=180°，
∴∠BON+∠AOM=90°，
∴∠MON=90°，
∴ON⊥OM；
②如图④，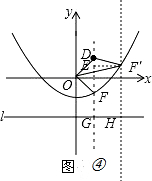

作F′H⊥l于H，DF⊥l于G，交抛物线与F，作F′E⊥DG于E，
∴∠EGH=∠GHF′=∠F′EG=90°，FO=FG，F′H=F′O，
∴四边形GHF′E是矩形，FO+FD=FG+FD=DG，F′O+F′D=F′H+F′D
∴EG=F′H，
∴DE＜DF′，
∴DE+GE＜HF′+DF′，
∴DG＜F′O+DF′，
∴FO+FD＜F′O+DF′，
∴F是所求作的点．
∵D（1，1），
∴F的横坐标为1，
∴F（1，-$\frac{3}{4}$）．

点评 本题考查了二次函数综合题，运用待定系数法求二次函数的解析式，勾股定理的运用，平行线的性质的运用，等腰三角形的性质的运用，垂直的判定及性质的运用，解答时求出函数的解析式是关键．