
科目:初中数学 来源: 题型:解答题
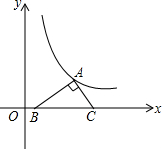 如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.
如图,将一个30°的直角三角形板的斜边BC放在x轴上,直角顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,AB=1,求点C的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
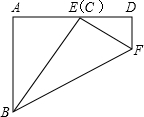 在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
在一次数学课上,小明同学把一个宽为3(AB=3)的矩形ABCD折成如图所示的图形,点C刚好落在AD边上的点E处,若∠DEF=40°,求矩形的长AD.(精确到0.1)(参考数据:sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是6×6的网格图,任意上下左右相邻的两点间的距离都是1,则以网格图中的格点为顶点画等腰直角三角形,共能画出面积互不相等的等腰直角三角形的个数为( )
如图,是6×6的网格图,任意上下左右相邻的两点间的距离都是1,则以网格图中的格点为顶点画等腰直角三角形,共能画出面积互不相等的等腰直角三角形的个数为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com