
分析 先化简分式,然后再化简a的值,从而可求出原式的值.
解答 解:原式=$\frac{a-6}{(a+2)(a-2)}$×$\frac{a-2}{a}$-$\frac{3}{a+2}$×$\frac{a-2}{a}$
=$\frac{a-6}{a(a+2)}$-$\frac{3(a-2)}{a(a+2)}$
=$-\frac{2}{a+2}$
由于a=2017°+(-$\frac{1}{5}$)-1+$\sqrt{27}$tan30°,
∴a=1-5+3=-1
∴原式=-$\frac{2}{-1+2}$=-2
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
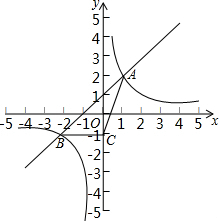 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x-5 | B. | y=2x+5 | C. | y=2x+8 | D. | y=2x-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
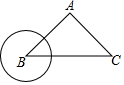 如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$.
如图,△ABC中,AB=AC=5,BC=8,⊙B的半径为2,圆心B从点B出发,沿着线段BC向右平移,⊙B随着点B的平移而以相同的速度平移.当⊙B与边AB相切时,⊙B平移的距离是$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
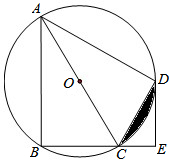 如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.
如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com