
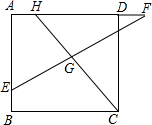
 对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.分析 (1)假命题;根据命题画图验证即可;
(2)连接CE、CF,易证△CBE≌△CDF,则CE=CF,∠BCE=∠DCE,得到△ECF是等腰直角三角形,又G是EF的中点,所以GE=GC,∠EGC=90°,于是四边形BCGE是奇特四边形;
(3)①过点G作MN∥AB,GQ∥AD,易得△GQE≌△GMC,所以四边形BMGQ是正方形,S四边形BCGE=S正方形BMGQ,从而求出GQ=GM=AN=4,由平行线等分线段知,N是AF中点,得到AF=x+y=8;
②由x+y=8,得y=8-x,代入x+xy,利用二次函数的最值得x+xy取最大值时x的值,运用勾股定理和相似求出FH的长.
解答 解:(1)假命题,如图,AB=AC,∠ABD=∠ACD,又DC=DB,明显四边形ABDC不是正方形.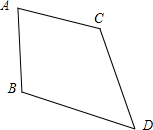
(2)连接CE,CF∵四边形ABCD是正方形,
∴BC=DC,∠EBC=∠FDC=90°,
在△EBC和△FDC中,
$\left\{\begin{array}{l}{BC=DC}\\{∠EBC=∠FDC=90°}\\{BE=DF}\end{array}\right.$
∴△CBE≌△CDF(SAS)
∴CE=CF,∠BCE=∠DCE
∴∠ECF=90°,
∵G是EF的中点,
∴GE=GC,∠EGC=90°,
∵GE=GC,∠EGC=∠B=90°
∴四边形BCGE是奇特四边形;
(3)①过点G作MN∥AB,GQ∥AD,
∴△GQE≌△GMC(AAS)
∴GQ=GM,
∴四边形BMGQ是正方形,S四边形BCGE=S正方形BMGQ,
∵四边形BCGE的面积是16,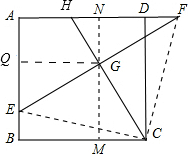
∴S正方形BMGQ=16
∴GQ=GM=AN=4,
∵G是EF的中点,
∴AN=FN=4,
∴AF=8
∵BE=DF,BC=AD,
∴BE+BC=AF=8
∵BC=x,BE=y
∴x+y=8;
②由①知y=8-x,
∴x+xy=x+x(8-x)=-x2+9x=-(x-$\frac{9}{2}$)2+$\frac{81}{4}$,
∴x+xy取最大值时,x=BC=4.5,y=BE=3.5
∴CE=CF=$\sqrt{(\frac{9}{2})^{2}+(\frac{7}{2})^{2}}$=$\frac{\sqrt{130}}{2}$,
∴FG=$\frac{\sqrt{260}}{4}$
∵Rt△FGH∽Rt△FNG
∴FG2=FN•FH
∵FN=4,FG=$\frac{\sqrt{260}}{4}$,
∴FH=$\frac{65}{16}$.
点评 本题主要考查了正方形的判定与性质,三角形的全等,三角形的相似,勾股定理,二次函数的性质.本题综合性较强,有一定难度.


科目:初中数学 来源: 题型:解答题
 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≤2或m≥3 | B. | m≤3或m≥4 | C. | 2<m<3 | D. | 3<m<4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| ax2+bx+c | … | -3 | 2 | 3 | 0 | -7 | … |
| A. | 有两个不相等实根 | B. | 有两个相等实根 | ||
| C. | 只有一个实根 | D. | 无实根 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+2y=7 | B. | -2x+y=-3 | C. | 6x+y=8 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com