
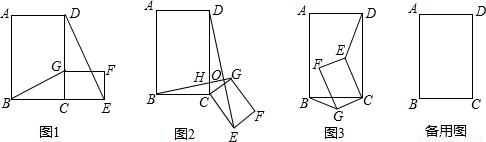
 ,AB=8,BC=4,△BDF的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
,AB=8,BC=4,△BDF的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.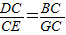 ,从而可以得到△BCG∽△DCE,再利用角相等通过代换就可以得出结论;
,从而可以得到△BCG∽△DCE,再利用角相等通过代换就可以得出结论;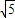 为半径的圆,所以△BDF的BD边上的高就是点F到BD的距离,也就是BD到圆上的点的距离,有最大值和最小值,最大值为点C到BD的距离与圆的半径的和,最小值为点C到BD的距离与圆的半径的差,再利用三角形的面积公式求解即可.
为半径的圆,所以△BDF的BD边上的高就是点F到BD的距离,也就是BD到圆上的点的距离,有最大值和最小值,最大值为点C到BD的距离与圆的半径的和,最小值为点C到BD的距离与圆的半径的差,再利用三角形的面积公式求解即可. ,
,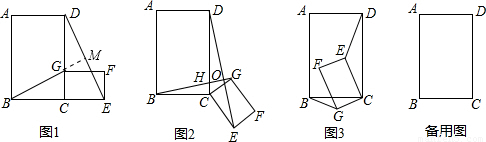 ∴BG⊥DE;
∴BG⊥DE;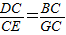 ,
,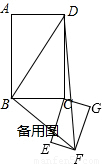 (3)△BDF的面积是否存在最大值与最小值.理由如下:
(3)△BDF的面积是否存在最大值与最小值.理由如下: ,BD=
,BD=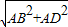 =4
=4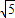 ,
, ,
,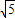 为半径的圆.
为半径的圆.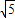 h=8×4,
h=8×4, ,
,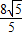 +
+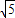 =
=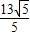 时,△BDF的面积有最大值,
时,△BDF的面积有最大值,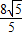 -
-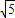 =
=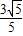 时,△BDF的面积有最小值,
时,△BDF的面积有最小值, ×4
×4 ×
×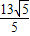 =26,
=26, ×4
×4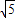 ×
×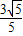 =6.
=6.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
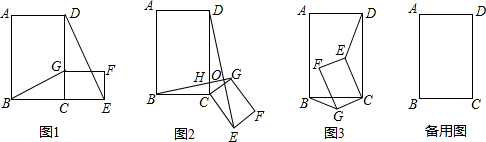
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
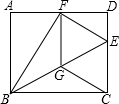 使点E落在BE上的点G处,连接CG.
使点E落在BE上的点G处,连接CG.查看答案和解析>>
科目:初中数学 来源: 题型:
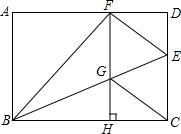 如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
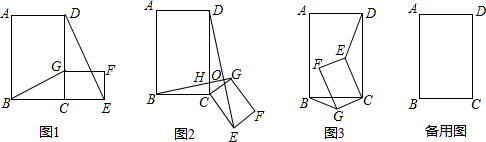
 ,AB=8,BC=4,△BDF的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
,AB=8,BC=4,△BDF的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com