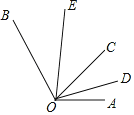
[题目]如图.∠AOB=130°.射线OC是∠AOB内部任意一条射线.OD.OE分别是∠AOC.∠BOC的角平分线.下列叙述正确的是( )A. ∠DOE的度数不能确定 B. ∠AOD=∠EOCC. ∠AOD+∠BOE=65° D. ∠BOE=2∠COD 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，∠AOB=130°，射线OC是∠AOB内部任意一条射线，OD、OE分别是∠AOC、∠BOC的角平分线，下列叙述正确的是（　　）

A. ∠DOE的度数不能确定 B. ∠AOD=∠EOC

C. ∠AOD+∠BOE=65° D. ∠BOE=2∠COD

【答案】C

【解析】

依据OD、OE分别是∠AOC、∠BOC的平分线，即可得出∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°，结合选项得出正确结论．

∵OD、OE分别是∠AOC、∠BOC的平分线，∴∠AOD=∠COD，∠EOC=∠BOE．

又∵∠AOD+∠BOE+∠EOC+∠COD=∠AOB=130°，∴∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°．

故选C．

练习册系列答案

暑假作业新世界出版社系列答案

创新成功学习快乐暑假云南科技出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】列方程解应用题：

（1）一个箱子，如果装橙子可以装18个，如果装梨可以装16个，现共有橙子、梨400个，而且装梨的箱子是装橙子箱子的2倍．请算一下，装橙子和装梨的箱子各多少个？

（2）一群小孩分一堆苹果，每人3个多7个，每人4个少3个，求有几个小孩？几个苹果？

（3）一架飞机在两城之间飞行，风速为24千米/时．顺风飞行需要2小时50分，逆风飞行需要3小时，求无风时飞机的速度和两城之间的航程．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】列方程（组）解应用题

(1)某中学组织初一学生春游，原计划租用45座汽车若干辆，但有15人没有座位；若租用同样数量的60座汽车，则比45座汽车多出一辆无人乘坐，但其余客车恰好坐满．问初一年级人数是多少？原计划租用45座汽车多少辆？

(2)《孙子算经》是中国古代重要的数学著作，记有许多有趣而又不乏技巧的算术程式，其中记载：“今有甲、乙二人，持钱各不知数．甲得乙中半，可满四十八．乙得甲太半，亦满四十八，问甲、乙二人原持钱各几何？”译文：“甲，乙两人各有若干钱．如果甲得到乙所有钱的一半，那么甲共有钱48文，如果乙得到甲所有钱的，那么乙也共有钱48文，问甲，乙二人原来各有多少钱？”