
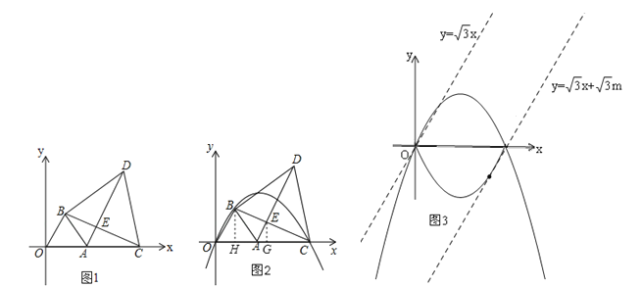
【题目】如图1,点A坐标为(2,0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A右侧,连接BC,以BC为边在第一象限内作等边△BCD,连接AD交BC于E.
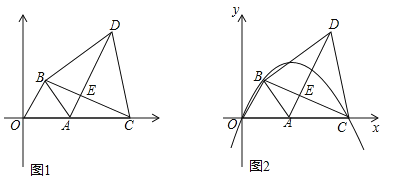
(1)①直接回答:△OBC与△ABD全等吗?
②试说明:无论点C如何移动,AD始终与OB平行;
(2)当点C运动到使AC2=AEAD时,如图2,经过O、B、C三点的抛物线为y1.试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的条件下,将y1沿x轴翻折得y2,设y1与y2组成的图形为M,函数![]() 的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
【答案】(1)①△OBC与△ABD全等;②证明见解析;(2)P(3,![]() )或(﹣2,
)或(﹣2,![]() );(3)﹣
);(3)﹣![]() ≤m<0.
≤m<0.
【解析】
试题分析:(1)①利用等边三角形的性质证明△OBC≌△ABD;
②证明∠OBA=∠BAD=60°,可得OB∥AD;
(2)首先证明DE⊥BC,再求直线AE与抛物线的交点就是点P,所以分别求直线AE和抛物线y1的解析式组成方程组,求解即可;
(3)先画出如图3,根据图形画出直线与图形M有个公共点时,两个边界的直线,上方到![]() ,将
,将![]() 向下平移即可满足l与图形M有3个公共点,一直到直线l与y2相切为止,主要计算相切时,列方程组,确定△≥0时,m的值即可.
向下平移即可满足l与图形M有3个公共点,一直到直线l与y2相切为止,主要计算相切时,列方程组,确定△≥0时,m的值即可.
试题解析:(1)①△OBC与△ABD全等,理由是:如图1,∵△OAB和△BCD是等边三角形,∴∠OBA=∠CBD=60°,OB=AB,BC=BD,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,∴△OBC≌△ABD(SAS);
②∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,∴∠OBA=∠BAD,∴OB∥AD,∴无论点C如何移动,AD始终与OB平行;
(2)如图2,∵AC2=AEAD,∴![]() ,∵∠EAC=∠DAC,∴△AEC∽△ACD,∴∠ECA=∠ADC,∵∠BAD=∠BAO=60°,∴∠DAC=60°,∵∠BED=∠AEC,∴∠ACB=∠ADB,∴∠ADB=∠ADC,∵BD=CD,∴DE⊥BC,Rt△ABE中,∠BAE=60°,∴∠ABE=30°,∴AE=
,∵∠EAC=∠DAC,∴△AEC∽△ACD,∴∠ECA=∠ADC,∵∠BAD=∠BAO=60°,∴∠DAC=60°,∵∠BED=∠AEC,∴∠ACB=∠ADB,∴∠ADB=∠ADC,∵BD=CD,∴DE⊥BC,Rt△ABE中,∠BAE=60°,∴∠ABE=30°,∴AE=![]() AB=
AB=![]() ×2=1,Rt△AEC中,∠EAC=60°,∴∠ECA=30°,∴AC=2AE=2,∴C(4,0),等边△OAB中,过B作BH⊥x轴于H,∴BH=
×2=1,Rt△AEC中,∠EAC=60°,∴∠ECA=30°,∴AC=2AE=2,∴C(4,0),等边△OAB中,过B作BH⊥x轴于H,∴BH=![]() =
=![]() ,∴B(1,
,∴B(1,![]() ),设y1的解析式为:y=ax(x﹣4),把B(1,
),设y1的解析式为:y=ax(x﹣4),把B(1,![]() )代入得:
)代入得:![]() =a(1﹣4),a=﹣
=a(1﹣4),a=﹣![]() ,∴设y1的解析式为:y1=﹣
,∴设y1的解析式为:y1=﹣![]() x(x﹣4)=
x(x﹣4)=![]() ,过E作EG⊥x轴于G,Rt△AGE中,AE=1,∴AG=
,过E作EG⊥x轴于G,Rt△AGE中,AE=1,∴AG=![]() AE=
AE=,EG=
![]() =
=![]() ,∴E(
,∴E(![]() ,
,![]() ),设直线AE的解析式为:y=kx+b,把A(2,0)和E(
),设直线AE的解析式为:y=kx+b,把A(2,0)和E(![]() ,
,![]() )代入得:
)代入得: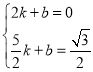 ,解得:
,解得: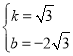 ,∴直线AE的解析式为:
,∴直线AE的解析式为:![]() ,则
,则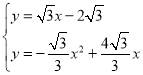 ,解得:
,解得: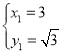 ,
,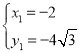 ,∴P(3,
,∴P(3,![]() )或(﹣2,
)或(﹣2,![]() );
);
(3)如图3,y1=![]() =
=![]() ,顶点(2,
,顶点(2,![]() ),∴抛物线y2的顶点为(2,﹣
),∴抛物线y2的顶点为(2,﹣![]() ),∴y2=
),∴y2=![]() ,当m=0时,
,当m=0时,![]() 与图形M两公共点,当y2与l相切时,即有一个公共点,l与图形M有3个公共点,则:
与图形M两公共点,当y2与l相切时,即有一个公共点,l与图形M有3个公共点,则: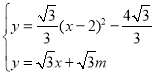 ,
,![]() ,x2﹣7x﹣3m=0,△=(﹣7)2﹣4×1×(﹣3m)≥0,m≥﹣
,x2﹣7x﹣3m=0,△=(﹣7)2﹣4×1×(﹣3m)≥0,m≥﹣![]() ,∴当l与M的公共点为3个时,m的取值是:﹣
,∴当l与M的公共点为3个时,m的取值是:﹣![]() ≤m<0.
≤m<0.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S2017的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车收费标准为:起步价(3千米以内或3千米)10元,3千米后每千米价1.8元,则某人乘坐出租车x(x>3)千米需付费( )元.
A. 10+1.8xB. 3+1.8x
C. 10+1.8(x﹣3)D. 3+1.8(x﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD= 120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 . 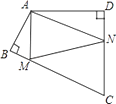
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3 . 若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.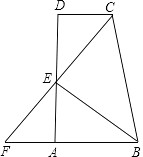
(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A,B,C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点
B.BC中点
C.AC中点
D.∠C的平分线与AB的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com