练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．一元二次方程：x（2x-1）=x的解是x1=0，x2=1．

    分析 移项、提公因式得到两个因式的积的形式，得到方程的解．

    解答 解：移项得，x（2x-1）-x=0，
    提公因式得，x（2x-2）=0，
    即x=0，2x-2=0，
    x1=0，x2=1，
    故答案为：x1=0，x2=1．

    点评 本题考查的是用因式分解法解一元二次方程，不要两边同除x导致丢根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．如图，AB∥CD，EF平分∠AEG，若∠FGE=40°，那么∠EFG的度数为（　　）
    A．35°B．40°C．70°D．140°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

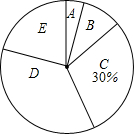    13．今年5月份，某校九年级学生参加了南宁市中考体育考试，为了了解该校九年级（1）班同学的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：
    （1）求全班学生人数和m的值．
    （2）直接学出该班学生的中考体育成绩的中位数落在哪个分数段．
    （3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
    分组分数段（分）频数
    A36≤x＜412
    B41≤x＜465
    C46≤x＜5115
    D51≤x＜56m
    E56≤x＜6110

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

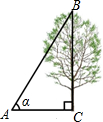    15．如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，则树高BC为（　　）米．
    A．7tanαB．$\frac{7}{tanα}$C．7sinαD．7cosα

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

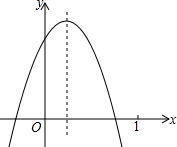    2．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①方程ax2+bx+c=0的两根之和大于0； ②a+b＜0；③y随x的增大而增大；④a-b+c＜0，⑤2a-b＞0． 其中正确的个数（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知点P（x0，y0）和直线kx-y+b=0（由y=kx+b变形而得），则点P到直线kx-y+b=0的距离d可用公式d=$\frac{{|{k{x_0}-{y_0}+b}|}}{{\sqrt{1+{k^2}}}}$计算．例如：求点P（-2，1）到直线y=x+1的距离．解：由直线y=x+1可得x-y+1=0，k=1，b=1．则点P到直线y=x+1的距离为d=$\frac{{|{k{x_0}-{y_0}+b}|}}{{\sqrt{1+{k^2}}}}$=$\frac{{|{1×（-2）-1+1}|}}{{\sqrt{1+{1^2}}}}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$．根据以上材料，解决下列问题：
    （1）请求出点P（1，1）到直线y=3x-12的距离；
    （2）已知互相平行的直线y=x-2与y=x+b之间的距离是3$\sqrt{2}$，试求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图1，已知直线l1平行l2，且l3与l1、l2分别交于A、B两点，l4与l1、l2分别交于C、D两点，点P在直线AB上．
    （1）当点P在A、B两点之间时，试猜想∠CPD与∠1、∠2的数量关系，并说明理由．
    （2）如果点P在A、B两点之间运动时，问∠CPD与∠1、∠2的关系是否发生变化？
    （3）如果点P在A、B两点外侧运动（如图2）时，试探究∠CPD与∠1、∠2的关系（点P和A、B不重合），并写出探究过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

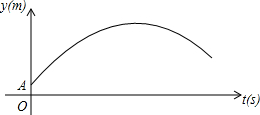    16．如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出（点A在y轴上），足球的飞行高度y（单位：m）与飞行时间t（单位：s）之间满足函数关系y=at2+5t+c，已知足球飞行0.8s时，离地面的高度为3.5m．
    （1）足球飞行的时间是多少时，足球离地面最高？最大高度是多少？
    （2）若足球飞行的水平距离x（单位：m）与飞行时间t（单位：s）之间具有函数关系x=10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？

    查看答案和解析>>

    同步练习册答案