
【题目】综合与实践
如图,根据给出的数轴,解答下面的问题:
![]()
(1)已知点![]() 表示的数分别为6,-4,观察数轴,与点
表示的数分别为6,-4,观察数轴,与点![]() 距离为5的点所表示的数是 ,
距离为5的点所表示的数是 ,![]() 两点之间的距离为 ;
两点之间的距离为 ;
(2)若点![]() 到点
到点![]() ,点
,点![]() 的距离相等,观察数轴并结合所学知识求点
的距离相等,观察数轴并结合所学知识求点![]() 表示的数;
表示的数;
(3)在(2)的条件下,若动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒.则点
秒.则点![]() 表示的数是多少(用含字母
表示的数是多少(用含字母![]() 的式子表示);当
的式子表示);当![]() 等于多少秒时,
等于多少秒时,![]() 之间的距离为3个单位长度.
之间的距离为3个单位长度.
【答案】(1)1或-9,10;(2)点![]() 表示的数为1;(3)1或4
表示的数为1;(3)1或4
【解析】
(1)分在点B左边和右边两种情况考虑;![]() 两点之间的距离为点A表示的数-点B表示的数;
两点之间的距离为点A表示的数-点B表示的数;
(2)分别表示出B、C两点之间的距离和C、A两点之间的距离,据此列出方程求解;
(3)先表示出点P运动的路程为2t,于是可以表示点![]() 表示的数;分“点
表示的数;分“点![]() 在点
在点![]() 的左边和点
的左边和点![]() 在点
在点![]() 的右边”两种情况列方程求解.
的右边”两种情况列方程求解.
解:(1)与点![]() 距离为5的点所表示的数是-4+5=1或-4-5=-9.
距离为5的点所表示的数是-4+5=1或-4-5=-9.
![]() 两点之间的距离为6-(-4)=10;
两点之间的距离为6-(-4)=10;
故答案是:1或-9,10;
(2)观察数轴,可知点![]() 一定在点
一定在点![]() 与点
与点![]() 之间,设点
之间,设点![]() 表示的数为
表示的数为![]() ,
,
则有![]()
解方程,得![]()
即点![]() 表示的数为1.
表示的数为1.
(3)点![]() 表示的数是
表示的数是![]() .
.
依题意得:当点![]() 在点
在点![]() 的左边时,
的左边时,![]() ,即
,即![]() ,则
,则![]() ;
;
当点![]() 在点
在点![]() 的右边时,
的右边时,![]() ,即
,即![]() ,则
,则![]() .
.
综上所述,当![]() 等于1或4秒时,
等于1或4秒时,![]() 之间的距离为3个单位长度.
之间的距离为3个单位长度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
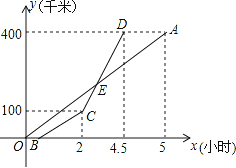
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )
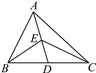
A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小王星期天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接八位乘客的行车里程(单位:![]() ):-3,+6,-1,-2,+4,-2,+5,-4.
):-3,+6,-1,-2,+4,-2,+5,-4.
问:(1)将最后一位乘客送到目的地时,小王在什么位置?
(2)若汽车耗油量为![]() ,这天上午小王接送乘客,出租车共耗油多少升?
,这天上午小王接送乘客,出租车共耗油多少升?
(3)若出租车的起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.5元,则小王这天上午共得车费多少元?
),超过部分每千米1.5元,则小王这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王叔叔在太原市小店区买了一套商品房,他准备用1万元将地面铺上地砖,这套住宅的建筑平面图(由多个长方形组成)如图所示(图中长度单位:![]() ),请据图解答下列问题.
),请据图解答下列问题.
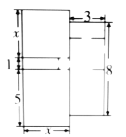
(1)用含![]() 的代数式表示这所住宅的总面积;
的代数式表示这所住宅的总面积;
(2)某公司地砖报价为每平米200元,若![]() ,在现有条件下,王叔叔是否会选择该公司铺地砖?请说明理由.
,在现有条件下,王叔叔是否会选择该公司铺地砖?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
已知:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
试说明:∠EGF=90°.
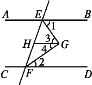
解:因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+ =180°( ).
又因为EG平分∠BEF(已知),
所以∠1=![]() ∠ ( ).
∠ ( ).
又因为FG平分∠EFD(已知),
所以∠2=![]() ∠ ( ),
∠ ( ),
所以∠1+∠2=![]() ( + ).
( + ).
所以∠1+∠2=90°.
所以∠3+∠4=90°( ),即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,8为半径的圆与
为圆心,8为半径的圆与![]() 轴交于
轴交于![]() ,
,![]() 两点,过
两点,过![]() 作直线
作直线![]() 与
与![]() 轴负方向相交成
轴负方向相交成![]() 的角,且交
的角,且交![]() 轴于
轴于![]() 点,以点
点,以点![]() 为圆心的圆与
为圆心的圆与![]() 轴相切于点
轴相切于点![]() .
.
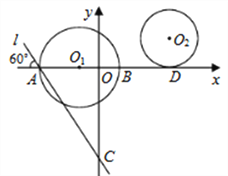
(1)求直线![]() 的解析式;
的解析式;
(2)将![]() 以每秒1个单位的速度沿
以每秒1个单位的速度沿![]() 轴向左平移,当
轴向左平移,当![]() 第一次与
第一次与![]() 外切时,求
外切时,求![]() 平移的时间.
平移的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
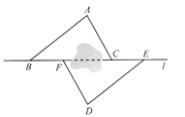
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com