
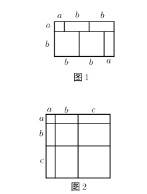
【题目】如图1,小明用1张边长为![]() 的正方形,2张边长
的正方形,2张边长![]() 为的正方形,3张边长分别为
为的正方形,3张边长分别为![]() 的长方形纸片拼成一个长为
的长方形纸片拼成一个长为![]() ,宽为
,宽为![]() 的长方形,它的面积为
的长方形,它的面积为![]() ,于是,我们可以得到等式
,于是,我们可以得到等式![]()
请解答下列问题:
(1)根据图2,写出一个代数恒等式;
(2)利用(1)中所得的结论,解决下面的问题:已知![]() ,求
,求![]() 的值.
的值.
(3)小明又用4张边长为![]() 的正方形,3张边长为
的正方形,3张边长为![]() 的正方形,8张边长分别为
的正方形,8张边长分别为![]() 的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)同题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.
∴∠APE=180°-∠PAB=180°-130°=50°.
∵AB∥CD.∴PE∥CD.
…………
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的思路,解答下面的问题:
如图3,AD∥BC,点P在射线OM上运动,∠MDP=∠α,∠BCP=∠β.
①当点P在A、B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.
②当点P在A、B两点外侧时(点P与点O不重合),请直接写出∠CPD,∠α,∠β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一股民在上星期五买进某公司股票1000股,每股27元,下表为本星期内每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股多少元?
星期三收盘时,每股多少元?
![]() 本星期内每股最低价多少元?
本星期内每股最低价多少元?
![]() 本周星期几抛售,获利最大,最大是多少?
本周星期几抛售,获利最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.
(1)小明和小红玩摸球游戏,规定每人摸球后再将摸到的球放回去为一次游戏.若摸到黑球小明获胜,摸到黄球小红获胜,这个游戏对双方公平吗?请说明你的理由;
(2)现在裁判想从袋中取出若干个黑球,并放入相同数量的黄球,使得这个游戏对双方公平,问取出了多少黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数 ![]() (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 ![]() 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我校某班同学随机抽取的我国100座城市2017年某天当地pm2.5值的情况的条形统计图,那么本次调查中,PM2.5值的中位数为微克/立方米.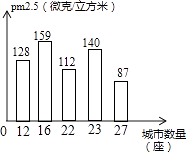
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com