
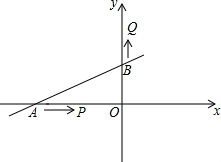
 直线y=$\frac{1}{2}$x+2交x轴于A,交y轴于B,P点从A点出发沿射线AO运动,同时Q从B点出发沿射线OB方向运动,速度均为1个单位/秒
直线y=$\frac{1}{2}$x+2交x轴于A,交y轴于B,P点从A点出发沿射线AO运动,同时Q从B点出发沿射线OB方向运动,速度均为1个单位/秒分析 (1)首先求出AO的长度是多少;然后分别求出BQ、AP的长度,再根据S△PBQ=BQ•OP÷2,求出S△PBQ的值是多少即可.
(2)根据题意,分两种情况:①当点P在AO上时;②当点P在x轴正半轴上时;然后分别求出0P、BQ的长度,根据S△PBQ=BQ•OP÷2=$\frac{5}{2}$,求出运动的时间t是多少即可.
(3)点P在线段OA上运动的过程中存在时间t,使S△PBQ最大.当点P在线段OA上运动时,0≤t≤4,应用配方法,可得S△PBQ=-$\frac{1}{2}$(t-2)2+2,据此判断出t=2时,S△PBQ最大即可.
解答 解:(1)如图1,
∵直线y=$\frac{1}{2}$x+2交x轴于A,交y轴于B,
∴A(-4,0)、B(0,2),
∴AO=4,
∵t=3,
∴BQ=1×3=3,AP=1×3=3,
∴S△PBQ=BQ•OP÷2=3×(4-3)÷2=1.5.
(2)①如图2,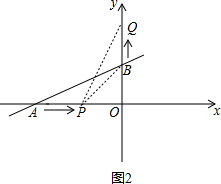
当点P在AO上时,
∵S△PBQ=$\frac{5}{2}$,
∴(4-t)t÷2=$\frac{5}{2}$,
整理,可得
t2-4t+5=0,
∵△=42-4×5=-4<0,
∴方程无解.
②如图3,
当点P在x轴正半轴上时,
∵S△PBQ=$\frac{5}{2}$,
∴(t-4)t÷2=$\frac{5}{2}$,
整理,可得
t2-4t-5=0,
解得t=5或t=-1(舍去),
∴当S△PBQ=$\frac{5}{2}$时,运动的时间t=5s.
综上,可得当S△PBQ=$\frac{5}{2}$时,运动的时间t=5s.
(3)点P在线段OA上运动的过程中存在时间t,使S△PBQ最大.
如图4,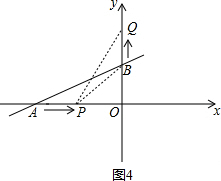
点P在线段OA上运动时,0≤t≤4,
∵S△PBQ=(4-t)t÷2=-$\frac{1}{2}$(t-2)2+2,
∴t=2时,S△PBQ最大=2,
∴点P在线段OA上运动的过程中存在时间t=2s,使S△PBQ最大是2.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了行程问题中各个量之间的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | x<2 | B. | x≤0 | C. | x≥0 | D. | x≥0且x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知反比例函数y1=$\frac{k}{x}$和二次函数y2=-x2+bx+c的图象都过点A(-1,2)
已知反比例函数y1=$\frac{k}{x}$和二次函数y2=-x2+bx+c的图象都过点A(-1,2)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
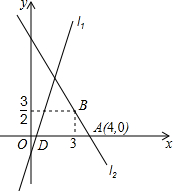 如图,直线l1的解析表达式为y=3x-3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
如图,直线l1的解析表达式为y=3x-3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com