
【题目】甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备
后,乙组的工作效率是原来的2倍.两组各自加工零件的数量![]() (件)与时间
(件)与时间![]() (时)的函数图
(时)的函数图
象如图所示.
(1)求甲组加工零件的数量y与时间![]() 之间的函数关系式.(2分)
之间的函数关系式.(2分)
(2)求乙组加工零件总量![]() 的值.(3分)
的值.(3分)
(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?(5分)

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:EDEA=ECEB;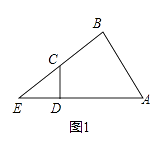
(2)如图2,若∠ABC=120°,cos∠ADC= ![]() ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;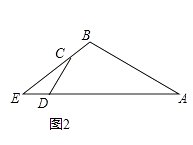
(3)如图3,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ![]() ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.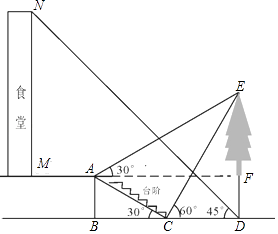
(1)求树DE的高度;
(2)求食堂MN的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一个月用水10 t以内(包括10 t)的用户,每吨收水费a元;一个月用水超过10 t的用户,10 t水仍按每吨a元收费,超过10 t的部分,按每吨b(b>a)元收费.设一户居民月用水x t,应交水费y元,y与x之间的函数关系如图所示.
(1)求a的值;某户居民上月用水8 t,应交水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,在射线BA上有一点D,连接CD,并以CD为边向上作等边△CDE,连接BE和AE.试判断下列结论:①AE=BD; ②AE与AB所夹锐夹角为60°;③当D在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2 .正确的序号有( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a,b,c在数轴上对应的点分别为A,B,C,且满足(a-1)2+|ab+3|=0,c=-2a+b.
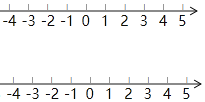
(1)分别求a,b,c的值;
(2)若点A和点B分别以每秒2个单位长度和每秒1个单位长度的速度在数轴上同时相向运动,设运动时间为t秒.
i)是否存在一个常数k,使得3BC-kAB的值在一定时间范围内不随运动时间t的改变而改变?若存在,求出k的值;若不存在,请说明理由.
ii)若点C以每秒3个单位长度的速度向右与点A,B同时运动,何时点C为线段AB的三等分点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
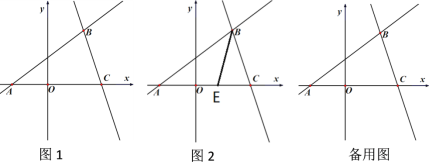
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴交于点A,且经过点B(2,m),点C(3,0).
轴交于点A,且经过点B(2,m),点C(3,0).
(1)求直线BC的函数解析式;
(2)在线段BC上找一点D,使得△ABO与△ABD的面积相等,求出点D的坐标;
(3)y轴上有一动点P,直线BC上有一动点M,若△APM是以线段AM为斜边的等腰直角三角形,求出点M的坐标;
(4)如图2,E为线段AC上一点,连结BE,一动点F从点B出发,沿线段BE以每秒1个单位运动到点E,再沿线段EA以每秒![]() 个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
个单位运动到A后停止,设点F在整个运动过程中所用时间为t,求t的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com