练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    函数y=kx-2与y=在同一坐标系中的大致图象是（   ）
    B

    试题分析：由题意分与两种情况，结合一次函数、反比例函数的性质分析即可.
    当时，的图象经过第一、三、四象限，的图象在一、三象限
    当时，的图象经过第二、三、四象限，的图象在二、四象限
    则符合条件的只有B选项，故选B.
    点评：解题的关键是熟练掌握一次函数的性质：当时，图象经过第一、二、三象限；当时，图象经过第一、三、四象限；当时，图象经过第一、二、四象限；当时，图象经过第二、三、四象限.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    已知反比例函数y=与一次函数y=mx+b的图象交于P(－2，1)和Q（1，n）两点．
    （1）求k、n的值；
    （2）求一次函数y=mx+b的解析式；
    （3）求△POQ的面积．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    有一道题目：已知一次函数，其中b<0，… ，与这段描述相符的函数图象可能是

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    某车间的甲、乙两名工人分别同时生产只同一型号的零件，他们生产的零件（只）与生产时间（分）的函数关系的图象如图所示。根据图象提供的信息解答下列问题：

    （1）甲每分钟生产零件_______只；乙在提高生产速度之前已生产了零件_______只；
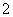    （2）若乙提高速度后，乙的生产速度是甲的倍，请分别求出甲、乙两人生产全过程中，生产的零件（只）与生产时间（分）的函数关系式；
    （3）当两人生产零件的只数相等时，求生产的时间；并求出此时甲工人还有多少只零件没有生产．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    某酒厂生产A，B两种品牌的酒，每天两种酒共生产700瓶，每种酒每瓶的成本和利润如下表所示，设每天共获利y元，每天生产A种品牌的酒x瓶．
     
    		A
    		B
    成本（元）
    		50
    		35
    利润（元）
    		20
    		15
    （1）请写出y关于x的关系式；
    （2）如果该厂每天至少投入成本30000元，那么每天至少获利多少元？
    （3）要使每天的利润率最大，应生产A，B两种酒各多少瓶？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

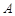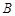    甲、乙两观光船分别从、两港同时出发，相向而行，两船在静水中速度相同，水流速度为5千米/小时，甲船逆流而行4小时到达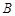港．下图表示甲观光船距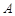港的距离（千米）与行驶时间（小时）之间的函数关系式，结合图象解答下列问题：

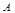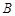    （1）、两港距离          千米，船在静水中的速度为          千米/小时；
    （2）在同一坐标系中画出乙船距港的距离（千米）与行驶时间（小时）之间的函数图象；
    （3）求出发几小时后，两船相距5千米．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    写出一条经过第一、二、四象限，且过点(，)的直线解析式            .

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    要使函数y=(2m-3)x+(3-m)的图像经过第一、二、三象限，则m的取值范围是___  _____.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

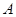    某饮料厂为了开发新产品，用种果汁原料和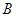种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制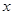千克，两种饮料的成本总额为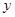元．
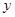    （1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出与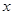之间的函数关系式；
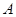    （2）若用19千克种果汁原料和17.2千克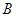种果汁原料试制甲、乙两种新型饮料，右表是试验的相关数据；请你列出关于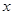且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，可使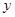值最小，最小值是多少？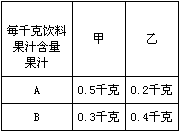

    查看答案和解析>>

    同步练习册答案