
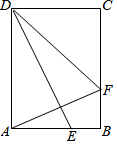
 在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )
在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )| A. | $\sqrt{2}-1$ | B. | 0.5 | C. | $\frac{2}{3}$ | D. | 1 |
分析 根据题意知AE=5t、BF=3t,由$\frac{AE}{AD}$=$\frac{t}{2}$=$\frac{BF}{AB}$且∠DAE=∠ABF=90°证△ADE∽△BAF得∠2=∠3,结合∠3=∠4、∠1=∠2得∠1=∠4,即可知DF=DA,从而得62+(10-3t)2=102,解之可得t的值,继而根据0≤5t≤6且0≤3t≤10取舍可得答案.
解答 解:如图,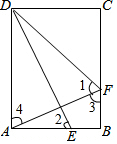
根据题意知,AE=5t,BF=3t,
∵BC=10cm,DC=6cm,
∴$\frac{AE}{AD}$=$\frac{5t}{10}$=$\frac{t}{2}$,$\frac{BF}{AB}$=$\frac{3t}{6}$=$\frac{t}{2}$,
∴$\frac{AE}{AD}=\frac{BF}{AB}$,
又∵∠DAE=∠ABF=90°,
∴△ADE∽△BAF,
∴∠2=∠3,
∵AD∥BC,
∴∠3=∠4,
∴∠2=∠4,
∵∠1=∠2,
∴∠1=∠4,
∴DF=DA,即DF2=AD2,
∵BF=3t,BC=10,
∴CF=10-3t,
∴DF2=DC2+CF2,即DF2=62+(10-3t)2,
∴62+(10-3t)2=102,
解得:t=$\frac{2}{3}$或t=6,
∵0≤5t≤6且0≤3t≤10,
∴0≤t≤$\frac{6}{5}$,
∴t=$\frac{2}{3}$,
故选:C.
点评 本题主要考查相似三角形的判定与性质、勾股定理、等角对等边和矩形的性质等知识点,根据对应边成比例且夹角相等得出两三角形相似继而由等角对等边得出关于t的方程是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:2017届江苏省无锡市九年级3月月考数学试卷(解析版) 题型:判断题
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
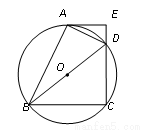
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
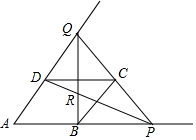 如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R
如图,四边形ABCD是边长为a的菱形,且∠A=60°,P是AB延长线上一动点,联结PC并延长交AD的延长线于点Q,联结BQ交PD于点R查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com