
| 课题 | 测量教学楼高度 | |
| 方案 | 一 | 二 |
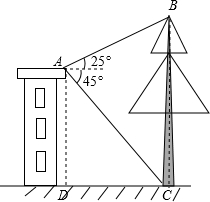
| 图示 |  | 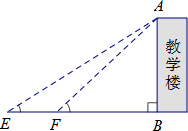 |
| 测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
| 参考数据 | sin22°≈0.37,cos22°≈0.93, tan22°≈0.40 sin13°≈0.22,cos13°≈0.97 tan13°≈0.23 | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 sin43°≈0.68,cos43°≈0.73,tan43°≈0.93 |
 即可得出CG的长,同理,在Rt△ACG中,根据tan∠ACG=
即可得出CG的长,同理,在Rt△ACG中,根据tan∠ACG=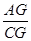 可得出AG的长,根据AB=AG+BG即可得出结论.
可得出AG的长,根据AB=AG+BG即可得出结论. 可得出FB的长,同理,在Rt△ABE中,由tan∠AEB=
可得出FB的长,同理,在Rt△ABE中,由tan∠AEB=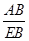 可求出EB的长,由EF=EB-FB且EF=10,可知
可求出EB的长,由EF=EB-FB且EF=10,可知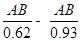 =10,故可得出AB的长.
=10,故可得出AB的长.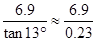 =30,
=30,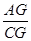 ,
, ,
,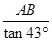 ≈
≈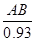 ,
,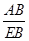 ,
,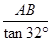 ≈
≈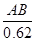 ,
,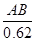 -
-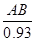 =10,解得AB=18.6≈19(米).
=10,解得AB=18.6≈19(米).

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:不详 题型:解答题
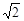 ≈1.414,
≈1.414,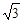 ≈1.732)
≈1.732)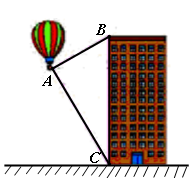
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com