练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
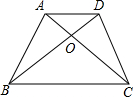
    7．如图，在梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，如果S△ACD：S△ABC=1：2，那么S△AOD：S△BOC是（　　）
    A．1：3B．1：4C．1：5D．1：6

    分析 首先根据S△ACD：S△ABC=1：2，可得AD：BC=1：2；然后根据相似三角形的面积的比的等于它们的相似比的平方，求出S△AOD：S△BOC是多少即可．

    解答 解：∵在梯形ABCD中，AD∥BC，而且S△ACD：S△ABC=1：2，
    ∴AD：BC=1：2；
    ∵AD∥BC，
    ∴△AOD～△BOC，
    ∵AD：BC=1：2，
    ∴S△AOD：S△BOC=1：4．
    故选：B．

    点评 此题主要考查了相似三角形的判定与性质的应用，以及梯形的特征和应用，要熟练掌握．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．至少含有a，b，c三个字母之一，且不含其他字母，系数为1的六次单项式共有28个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

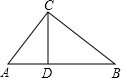    18．红星中学计划把一块形状如图所示的废弃荒地开辟为生物园，测得AC=75m，BC=100m，AB=125m．如果沿CD修一条水渠且D点在边AB上，水渠的造价为10元/m，问D点在什么位置时，水渠的造价最低？最低造价是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，在梯形ABCD中，AD∥BC，AC与BD相交于点O，如果BC=2AD，那么S△ADC：S△ABC的值为1：2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

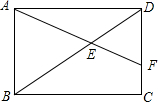    2．如图，矩形ABCD中，AB=$\sqrt{3}$，BC=$\sqrt{6}$，点E在对角线BD上，且BE=1.8，连接AE并延长交DC于点F．
    （1）求CF的长；
    （2）求$\frac{{S}_{△DEF}}{{S}_{△BEA}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．计算（-1）2016+（-1）2018所得的结果为（　　）
    A．0B．1C．-1D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

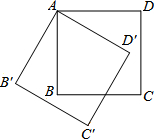    19．如图，将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置，旋转角为30°，则C点运动到C′点的路径长为（　　）
    A．$\frac{2}{3}$πcmB．$\frac{2\sqrt{2}}{3}$πmC．$\frac{2\sqrt{3}}{3}$cmD．$\frac{2\sqrt{5}}{3}$cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．“新禧”杂货店去批发市场购买某种新型儿童玩具，第一次用1200元购得玩具若干个，并以7元的价格出售，很快就售完．由于该玩具深受儿童喜爱，第二次进货时每个玩具的批发价已比第一次提高了20%，他用1500元所购买的玩具数量比第一次多10个，再按8元售完，问该老板两次一共赚了多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．已知关于x的方程（a-1）x|a|+1-2x-1=0是一元二次方程，则a的值为（　　）
    A．-1B．1C．0D．1或-1

    查看答案和解析>>

    同步练习册答案