
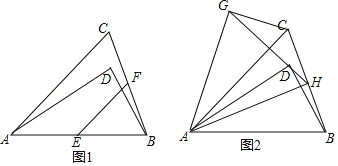
【题目】如图,在三角形ABC中,AB=AC,点D在△ABC内,且∠ADB=90°.
(1)如图1,若∠BAD=30°,AD=3![]() ,点E、F分别为AB、BC边的中点,连接EF,求线段EF的长;
,点E、F分别为AB、BC边的中点,连接EF,求线段EF的长;
(2)如图2,若△ABD绕顶点A逆时针旋转一定角度后能与△ACG重合,连接GD并延长交BC于点H,连接AH,求证:∠DAH=∠DBH.
【答案】(1)EF =3;(2)证明见解析.
【解析】
(1) 设BD=x,则AB=2x,由勾股定理得:![]() ,求出AB,再根据中位线性质求出EF;
,求出AB,再根据中位线性质求出EF;
(2) 在GH上取一点M,使GM=DH,由性质性质得△ADB≌△AGC,再证△CGM≌△BDH,得CM=BH,∠GCM=∠DBH,因为∠CMH=∠MGC+∠MCG,∠CHM=∠BDH+∠DBH,
所以∠CMH=∠CHM,可得CM=CH=BH,又AC=AB,所以AH⊥BC,∠AHB=90°=∠ADB,
又∠AOD=∠BOH,故∠DAH=∠DBH.
(1)解:如图1,在Rt△ABD中,∠BAD=30°,
∴AB=2BD,
设BD=x,则AB=2x,
由勾股定理得:![]() ,
,
x=3或﹣3(舍),
∴AB=2x=6,
∵AC=AB=6,
∵点E、F分别为AB、BC边的中点,
∴EF=![]() AC=3;
AC=3;
(2)证明:如图2,由旋转得:△ADB≌△AGC,
∴AG=AD,∠AGC=∠ADB=90°,CG=BD,
∴∠AGD=∠ADG,
∵∠ADB=90°,
∴∠ADG+∠BDH=90°,
∵∠AGD+∠MGC=90°,
∴∠MGC=∠BDH,
在GH上取一点M,使GM=DH,
∴△CGM≌△BDH,
∴CM=BH,∠GCM=∠DBH,
∵∠CMH=∠MGC+∠MCG,∠CHM=∠BDH+∠DBH,
∴∠CMH=∠CHM,
∴CM=CH=BH,
∵AC=AB,
∴AH⊥BC,即∠AHB=90°=∠ADB,
∵∠AOD=∠BOH,
∴∠DAH=∠DBH.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,①等腰三角形两腰上的高相等;②在空间中,垂直于同一直线的两直线平行;③两条直线被第三条直线所截,内错角相等;④一个角的两边与另一个角的两边分别平行, 则这两个角相等. 其中真命题的个数有 __________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 、
、![]() 与相交于点
与相交于点![]() ,形成了
,形成了![]() 个角.
个角.
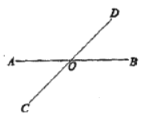
(1)图中,![]() 与
与![]() 有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.这样的邻补角还有以下几对,它们分别是____________、__________、______________.
(2)图中,![]() 与
与![]() 有一个公共顶点,且
有一个公共顶点,且![]() 的两边分别是
的两边分别是![]() 的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
的反向延长线,具有这种位置关系的两个角,互为对顶角.这样的对顶角还有一对,它们是________与___________.
(3)因为![]() ______________,
______________,![]() ____________所以
____________所以![]() ______
______![]() (填写
(填写![]() 或
或![]() 或
或![]() )理由是____________由此能得到的结论是:对顶角_____________
)理由是____________由此能得到的结论是:对顶角_____________
(4)用您所学知识可得![]() ___________(精确到度).
___________(精确到度).
查看答案和解析>>
科目:初中数学 来源: 题型:
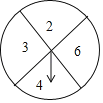
【题目】如图是一个转盘,转盘被平均分成4等分,即被分成4个大小相等的扇形,4个扇形分别标有数字2、3、4、6,指针的位置固定,转动转盘后任其自由停止,每次指针落在每个扇形的机会均等(若指针恰好落在分界线上则重转).
(1)若图中标有“2”的扇形至少绕圆心旋转n度能与标有“3”的扇形的起始位置重合,求n的值;
(2)现有一张电影票,兄弟俩商定通过转盘游戏定输赢(赢的一方先得).游戏规则是:姐妹俩各转动一次转盘,两次转动后,若指针所指扇形上的数字之和为小于8,则哥哥赢;若指针所指扇形上的数字之和不小于8,则弟弟赢.这个游戏规则对双方公平吗?请利用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为![]() ,剩下的水量为
,剩下的水量为![]() .下面能反映
.下面能反映![]() 与
与![]() 之间的关系的大致图象是( )
之间的关系的大致图象是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
数学中枚举法是一种重要归纳法也称为列举法、穷举法,是暴力策略的具体体现,又称为蛮力法.用枚举法解题时应该注意:
1、常常需要将对象进行恰当分类.
2、使其确定范围尽可能最小,逐个试验寻求答案.
正整数![]() 的末尾为5称为“威武数”,那么
的末尾为5称为“威武数”,那么![]() 的平方数为
的平方数为![]() 称为“平武数”.
称为“平武数”.
例:![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
……
由以上的枚举可以归纳得到的“平武数”特点是:
①“平武数”的末两位数字是25;
②去掉末两位数字25后,剩下部分组成的数字等于“平武数”去掉个位数字5后剩部分组成的数字与比此数大1的数之积.(如例中的括号内容)
(1)根据以上特点我们能够很快的推出一个四位数的“平武数”![]() 一共有___________个.
一共有___________个.
(2)同学们用学过的完全平方公式求证:当“威武数”![]() 为任意二位数时“平武数”
为任意二位数时“平武数”![]() 都满足以上特点.
都满足以上特点.
(3)已知“平武数”![]() 的首位数是2且小于六位,又满足
的首位数是2且小于六位,又满足![]() 的各位数字之和与
的各位数字之和与![]() 的各位数字之和相等,求出“平武数”
的各位数字之和相等,求出“平武数”![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
 (1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的![]() ;
;
(2)问两动点经过多长时间使得点P与点Q之间的距离为![]() ?若存在,
?若存在,
求出运动所需的时间;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com