
 如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,
如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,分析 (1)连接OE,根据矩形的性质求出∠CAE=∠BCA=∠DCE,求出∠DCE+∠CED=90°,即可求出∠AEO+∠CED=90°,求出∠OEC=90°,根据切线的判定推出即可;
(2)首先连接EF,易证得△ABC∽△EDC,然后由相似三角形的对应边成比例,求得DE的长,由勾股定理,求得AC的长,继而求得答案.
解答 (1)证明:连接OE,
∵OA=OE,
∴∠CAD=∠OEA,
∵四边形ABCD是矩形,
∴∠D=90°,BC∥AD,
∴∠BCA=∠CAD,
∵∠ACB=∠DCE,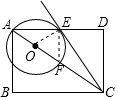
∴∠CAE=∠DCE,
∵∠DCE+∠CEB=180°-∠D=90°,
∴∠OEA+∠CED=90°,
∴∠OEC=180°-90°=90°,
∴CE是⊙O的切线;
(2)解:设⊙O与AC交于F,连接EF,
则∠AEF=90°,
∵∠B=∠D=90°,∠ACB=∠DCE,
∴△ABC∽△CDE,
∴$\frac{AB}{DE}=\frac{BC}{CD}$,即$\frac{3}{DE}=\frac{4}{3}$,
∴DE=$\frac{9}{4}$
∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵EF∥CD,
∴$\frac{AE}{AD}$=$\frac{AF}{AC}$,
∴AF=$\frac{35}{16}$,
∴⊙O的半径为$\frac{35}{32}$.
点评 此题考查了切线的性质、矩形的性质、相似三角形的判定与性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:选择题
| A. | m>n>k | B. | n>m>k | C. | k>m>n | D. | m>k>n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}k=0\\ b=0\end{array}\right.$ | B. | $\left\{\begin{array}{l}k=2\\ b=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}k=3\\ b=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=0\\ b=2\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一个立方体,现在要从图中的顶点A沿着立方体的棱走到顶点B,如果每个顶点最多只能经过一次,那么一共有( )种不同的走法.
如图是一个立方体,现在要从图中的顶点A沿着立方体的棱走到顶点B,如果每个顶点最多只能经过一次,那么一共有( )种不同的走法.| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
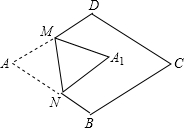 如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.
如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-3 | B. | x<-3 | C. | x≠-3 | D. | x≠3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com