练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，在三角形ABC中，已知AB=AC，D为BC边上的一点，且AB=BD，AD=CD，则∠ABC等于（　　）
    A．36°B．38°C．40°D．45°

    分析 根据等腰三角形的性质得到∠B=∠C，根据三角形外角的性质得到∠ADB=2∠C=2∠B，于是得到∠BDA=∠BAD=2∠B，在△ABD中利用三角形内角和定理可求出∠B．

    解答 解：∵AB=AC，
    ∴∠B=∠C，
    ∵CD=DA，
    ∴∠C=∠DAC，
    ∵BA=BD，
    ∴∠BDA=∠BAD=2∠C=2∠B，
    又∵∠B+∠BAD+∠BDA=180°，
    ∴5∠B=180°，
    ∴∠B=36°，
    故选A．

    点评 本题主要考查等腰三角形的性质，掌握等边对等角是解题的关键，注意三角形内角和定理和方程思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．“a2+4的算术平方根的相反数”用式子表示为-$\sqrt{{a}^{2}+4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在△ABC中，∠B=2∠C，AC=4$\sqrt{5}$，AB=5，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，在等腰△ABC中，AB=AC，∠A=20°，AB上一点D使AD=BC，过点D作DE∥BC且DE=AB，连接EC，则∠DCE的度数为（　　）
    A．80°B．70°C．60°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：$\sqrt{12}-\sqrt{2}$（$\sqrt{\frac{3}{2}}+\sqrt{24}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．已知△ABC∽△DEF，且AB：DE=1：2，则△ABC与△DEF的周长之比为（　　）
    A．1：2B．2：1C．1：4D．4：3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

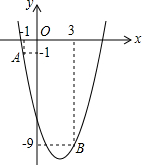    2．如图，已知二次函数y=ax2-4x+c的图象经过点A（-1，-1）和点B（3，-9）．
    （1）求该二次函数的表达式；
    （2）直接写出抛物线的对称轴及顶点坐标；
    （3）点P（m，m）与点Q均在该函效图象上（其中m＞0），且这两点关于抛物线的对称轴对称，求m的值及点Q到x轴的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：（-1）3+$\root{3}{8}$-（$\sqrt{2}$-1）0+$\sqrt{2}$×$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．我们在制作视力表时发现，每个“E”形图的长和宽相等（即每个“E”形图近似于正方形），如图，小明在制作视力表时，测得l1=14cm，l2=7cm，他选择了一张面积为4cm2的正方形卡纸，刚好可以剪得第②个小“E”形图．那么下面四张正方形卡纸中，能够刚好剪得第①个大“E”形图的是（　　）
    A．面积为8cm2的卡纸B．面积为16cm2的卡纸
    C．面积为32cm2的卡纸D．面积为64cm2的卡纸

    查看答案和解析>>

    同步练习册答案