
如下图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
(1) 点A的坐标是__________,点C的坐标是__________;
(2) 当t= 秒或 秒时,MN=![]() AC;
AC;
(3) 设△OMN的面积为S,求S与t的函数关系式;
(4) 探求(3)中得到的函数S有没有最大值?若有,求出最大值;若没有,要说明理由.
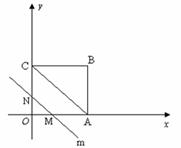
解:(1)(4,0),(0,3);
(2) 2,6;
(3) 当0<t≤4时,OM=t.
由△OMN∽△OAC,得![]() ,
,
∴ ON=![]() ,S=
,S=![]() .
.
当4<t<8时,
如图,
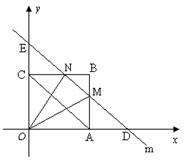
∵ OD=t,∴ AD= t-4.
方法一:
由△DAM∽△AOC,可得AM=![]() ,∴ BM=6-
,∴ BM=6-![]() .
.
由△BMN∽△BAC,可得BN=![]() =8-t,∴ CN=t-4.
=8-t,∴ CN=t-4.
S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积
=12-![]() -
-![]() (8-t)(6-
(8-t)(6-![]() )-
)-![]()
=![]() .
.
方法二:
易知四边形ADNC是平行四边形,∴ CN=AD=t-4,BN=8-t.
由△BMN∽△BAC,可得BM=![]() =6-
=6-![]() ,∴ AM=
,∴ AM=![]()
以下同方法一.
(4) 有最大值.
方法一:
当0<t≤4时,
∵ 抛物线S=![]() 的开口向上,在对称轴t=0的右边, S随t的增大而增大,
的开口向上,在对称轴t=0的右边, S随t的增大而增大,
∴ 当t=4时,S可取到最大值![]() =6;
=6;
当4<t<8时,
∵ 抛物线S=![]() 的开口向下,它的顶点是(4,6),∴ S<6.
的开口向下,它的顶点是(4,6),∴ S<6.
综上,当t=4时,S有最大值6.
方法二:
∵ S=
∴ 当0<t<8时,画出S与t的函数关系图像,如下图所示.
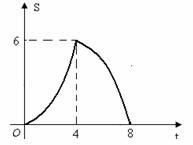
显然,当t=4时,S有最大值6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:云南省中考真题 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
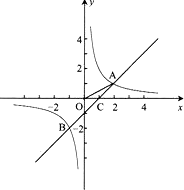
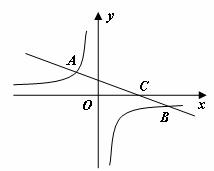
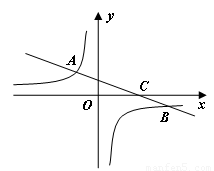
如下图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),
的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),![]() ,则此一次函数的解析式为 .
,则此一次函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北黄石卷)数学(解析版) 题型:填空题
如下图,在平面直角坐标系中,一次函数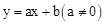 的图像与反比例函数
的图像与反比例函数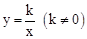 的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),
的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),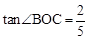 ,则此一次函数的解析式为 .
,则此一次函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源:2011-2012年北京市九年级上学期期中考试数学卷 题型:选择题
如下图,在平面直角坐标系中,以P (4,6)为位似中心,把△ABC缩小得到△DEF,若变换后,点A、B的对应点分别为点D、E,则点C的对应点F的坐标应为( ).

A. (4,2) B. (4,4) C. (4,5) D. (5,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com