练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：计算与化简
    （1） ﹣（﹣2）2+（﹣0.1）0；
    （2）（x﹣2）2﹣（x+3）（x﹣1）．

    【答案】
    （1）解：原式=3﹣4+1=0

    （2）解：原式=x2﹣4x+4﹣（x2+2x﹣3）=x2﹣4x+4﹣x2﹣2x+3=﹣6x+7
    【解析】（1）利用算数平方根的意义，非零数的零次幂意义可得出结果；（2）利用完全平方公式、多项式乘多项式法则可化简出结果.
    【考点精析】认真审题，首先需要了解零指数幂法则(零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）)，还要掌握多项式乘多项式(多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】王老师为学校购买运动会的奖品后，回学校向后勤处赵主任交账说：我买了两种书共105本，单价分别为8元和12元，买书前我领了1600元，现在还余518元．赵主任算了一下说：你肯定搞错了．

    （1）赵主任为什么说他搞错了，请你用方程组的知识给予解释；

    （2）王老师连忙拿出购物发票，发现的确弄错了，因为他还买了一个笔记本，但笔记本的单价已模糊不清，只能辨认出应为小于5元的整数，笔记本的单价可能为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，A(﹣1，5)，B(﹣1，0)，C(﹣4，3).

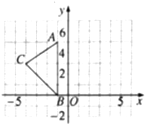
    ⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’，B’，C’分別是A，B，C的对应点，不写画法)；

    ⑵直接写出A’，B’，C’三点的坐标：A’ ( )，B’( )，C’( )；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，顶点为A的抛物线y=a（x+2）2﹣4交x轴于点B（1，0），连接AB，过原点O作射线OM∥AB，过点A作AD∥x轴交OM于点D，点C为抛物线与x轴的另一个交点，连接CD．

    （1）求抛物线的解析式；
    （2）若动点P从点O出发，以每秒1个单位长度的速度沿着射线OM运动，设点P运动的时间为t秒，问：当t为何值时，OB=AP；
    （3）若动点P从点O出发，以每秒1个单位长度的速度沿线段OD向点D运动，同时动点Q从点C出发，以每秒2个单位长度的速度沿线段CO向点O运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动时间为t秒，连接PQ．问：当t为何值时，四边形CDPQ的面积最小？并求此时PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠A=110°，在边AN上取B，C，使AB=BC．点P为边AM上一点，将△APB沿PB折叠，使点A落在角内点E处，连接CE，则∠BPE+∠BCE=°．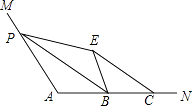

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把△ABC沿EF对折，叠合后的图形如图所示．若∠A=60°，∠1=85°，则∠2的度数（ ）

    A. 24°B. 25°C. 30°D. 35°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知ABCD，对角线AC，BD相较于点O，要使ABCD为矩形，需添加下列的一个条件是　　

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．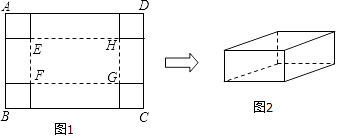

    （1）当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；
    （2）当EH：EF=7：2，且侧面积与底面积之比为9：7时，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了增强学生的身体素质，西南大学附中七年级学生在每天晚自习之后进行夜跑.在学期末的体育考试中，七年级的同学们表现出很好的体育素养，并取得了良好的体育成绩.为了了解七年级学生的体育考试情况，小明抽取了部分同学的体育考试成绩进行分析，体育成绩优、良、中、差分别记为并绘制了如下两幅不完整的统计表：

    （1）本次调查共调查了 名学生，并补全条形统计图；

    （2）扇形统计图中类所对应的扇形圆心角的度数是 度；

    （3）若七年级人数为人，请你估计体育成绩优、良的总人数．

    查看答案和解析>>

    同步练习册答案