
【题目】顶角为36°的等腰三角形称为黄金三角形,利用黄金三角形求![]() 的准确值.
的准确值.
【答案】![]()
【解析】
根据黄金三角形的顶角为36°,利用等腰三角形的性质求证∠GBC=∠BAC,∠C=∠C,从而得到△BGC∽△ABC,然后利用相似三角形的性质求其底与一腰之比即![]() ,作出黄金三角形顶角的平分线,解得等腰三角形三线合一的性质即可得出sin18°的值
,作出黄金三角形顶角的平分线,解得等腰三角形三线合一的性质即可得出sin18°的值
解:如图所示:做MN垂直平分AB交AC于点G,作∠BAC的平分线AD,
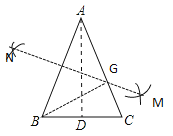
∵△ABC是黄金三角形,
∴∠BAC=36°,AB=AC,
∴AG=BG,∠GBA=∠BAG=36°,∠ABC=∠C=72°
∴∠GBC=36°,∠BGC=72°
设BC=x,AB=AC=y,
∴AG=BG=BC=x.
∵∠GBC=∠BAC,∠C=∠C,
∴△BGC∽△ABC,
∴![]() ,即
,即![]() ,
,
整理,得x2+xy-y2=0,
解得![]()
因为x、y均为正数,所以![]()
即![]() ,
,
作∠BAC的平分线AD,
则∠BAD=∠CAD=![]() ∠BAC=18°,AD⊥BC,BD=CD=
∠BAC=18°,AD⊥BC,BD=CD=![]() BC,
BC,
在Rt△ABD中,∠ADB=90°,
∴sin18°=sin∠BAD=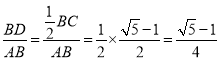 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0.
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根;
(2)当一矩形ABCD的对角线长为AC=![]() ,且矩形两条边AB和BC恰好是这个方程的两个根时,求矩形ABCD的周长.
,且矩形两条边AB和BC恰好是这个方程的两个根时,求矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.

(1)求此抛物线的解析式;
(2)求证:AO=AM;
(3)探究:
①当k=0时,直线y=kx与x轴重合,求出此时![]() 的值;
的值;
②试说明无论k取何值,![]() 的值都等于同一个常数.
的值都等于同一个常数.
查看答案和解析>>
科目:初中数学 来源: 题型:
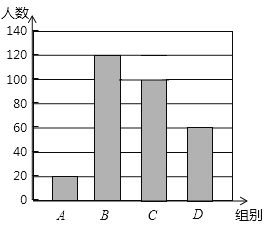
【题目】国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在 组内,中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
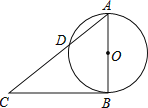
【题目】如图,AB是⊙O的直径,点C是⊙O外的一点,CB与⊙O相切于点B,AC交⊙O于点D,点E是![]() 上的一点(不与点A,B,D重合),若∠C=48°,则∠AED的度数为_____.
上的一点(不与点A,B,D重合),若∠C=48°,则∠AED的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
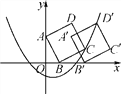
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=![]() x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤![]() .其中正确结论的是( )
.其中正确结论的是( )
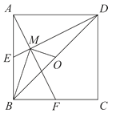
A. ①③④B. ②④⑤C. ①③⑤D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() 与点
与点![]() ,若在线段
,若在线段![]() 上存在点
上存在点![]() ,满足
,满足![]() ,则称点
,则称点![]() 为线段
为线段![]() 的“限距点”.
的“限距点”.

(1)如图,在平面直角坐标系![]() 中,若点
中,若点![]() .
.
①在![]() 中,是线段
中,是线段![]() 的“限距点”的是 ;
的“限距点”的是 ;
②点![]() 是直线
是直线![]() 上一点,若点
上一点,若点![]() 是线段
是线段![]() 的“限距点”,请求出点
的“限距点”,请求出点![]() 横坐标
横坐标![]() 的取值范围.
的取值范围.
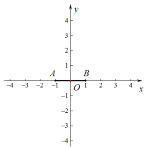
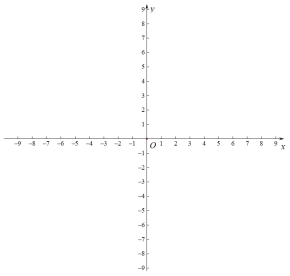
(2)在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
. ![]() 上存在线段
上存在线段![]() 的“限距点”,请求出
的“限距点”,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
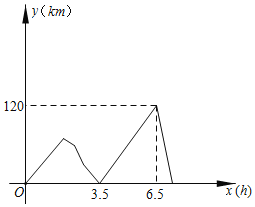
【题目】在一条笔直的公路上有A、B两地,甲、乙两车均从A地匀速驶向B地,甲车比乙车早出发2小时,出发后,甲车出现了故障停下来维修,半小时后继续以原速向B地行驶.当乙车到达B地后立刻提速50%返回,在返回途中第二次与甲车相遇.下图表示甲乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系.则当乙车第二次与甲车相遇时,甲车距离B地_____千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com