
【题目】(问题情境)一节数学课后,老师布置了一道课后练习题:
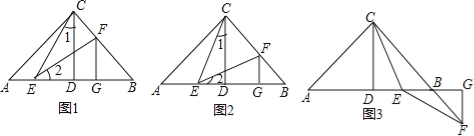
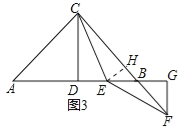
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
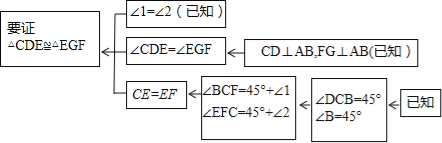
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
【答案】略;AE=![]() BF.
BF.
【解析】
试题(1)、先证明CE=EF,根据AAS即可证明△CDE≌△EGF;(2)、先证∠ACE=∠2,再证明△ACE≌△BEF,即可得出AE=BF;(3)、作EH⊥BC与H,设DE=x,求出AE=3x,再证出BF=![]() x,即可得出结论.
x,即可得出结论.
试题解析:(1)、∵AC=BC,∠ACB=90°, ∴∠A=∠B=45°, ∵CD⊥AB, ∴∠CDB=90°,
∴∠DCB=45°, ∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2, ∴∠ECF=∠EFC,
∴CE=EF, ∵CD⊥AB,FG⊥AB, ∴∠CDE=∠EGF=90°,
在△CDE和△EGF中,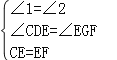 ,∴△CDE≌△EGF(AAS);
,∴△CDE≌△EGF(AAS);
(2)、由(1)得:CE=EF,∠A=∠B, ∵CE平分∠ACD, ∴∠ACE=∠1, ∵∠1=∠2,∴∠ACE=∠2,
在△ACE和△BEF中,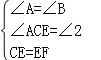 ,∴△ACE≌△BEF(AAS),∴AE=BF;
,∴△ACE≌△BEF(AAS),∴AE=BF;
(3)、AE=![]() BF,作EH⊥BC与H,如图3所示:
BF,作EH⊥BC与H,如图3所示:
设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x, 根据勾股定理得:BC=AC=2![]() x,
x,
∵∠ABC=45°,EH⊥BC, ∴BH=![]() x, ∴CH=BC﹣BH=
x, ∴CH=BC﹣BH=![]() x, ∵EC=EF, ∴FH=CH=
x, ∵EC=EF, ∴FH=CH=![]() x,
x,
∴BF=![]() x﹣
x﹣![]() x=
x=![]() x, ∴
x, ∴![]() , ∴AE=
, ∴AE=![]() BF.
BF.


科目:初中数学 来源: 题型:
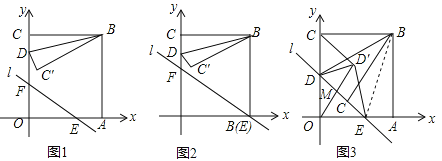
【题目】(2016浙江省衢州市)如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且![]() 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
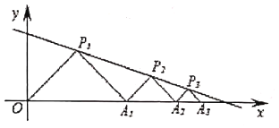
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,其直角顶点
,…都是等腰直角三角形,其直角顶点![]() ,
,![]() ,
,![]() ,…均在直线
,…均在直线![]() 上.设
上.设![]() ,
,![]() ,
,![]() ,…的面积分别为
,…的面积分别为![]() ,
,![]() ,
,![]() ,…,根据图形所反映的规律,
,…,根据图形所反映的规律,![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
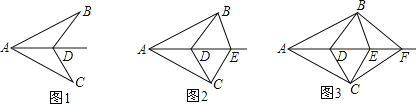
【题目】已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、BE、CE、BF、CF,图中有6对全等三角形;依此规律,第n个图形中有_____对全等三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数 1 至 2024 按一定规律排列成如图所示的 8 列,规定从上到下依次为第 1 行,第 2 行,第 3 行,…从左往右依次为第 1 列至第 8 列.
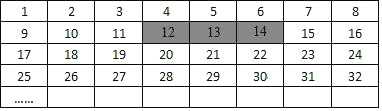
(1)数 56 在第 行 列 ;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为 x,则被框的三个数的和能否等于 2019?若能,请求出 x;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+![]() ∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-![]() ∠A.上述说法正确的个数是( )
∠A.上述说法正确的个数是( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
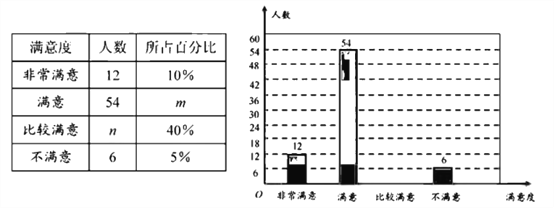
根据图表信息,解答下列问题:
(1)本次调查的总人数为 ,表中![]() 的值为 ;
的值为 ;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
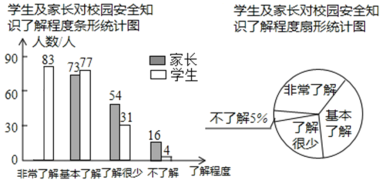
![]() 参与调查的学生及家长共有 人;
参与调查的学生及家长共有 人;
![]() 在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
![]() 在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com