
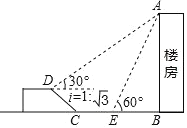
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面![]() 处测得楼房顶部
处测得楼房顶部![]() 的仰角为
的仰角为![]() ,沿坡面向下走到坡脚
,沿坡面向下走到坡脚![]() 处,然后向楼房方向继续行走10米到达
处,然后向楼房方向继续行走10米到达![]() 处,测得楼房顶部
处,测得楼房顶部![]() 的仰角为
的仰角为![]() .已知坡面
.已知坡面![]() 米,山坡的坡度
米,山坡的坡度![]() (坡度
(坡度![]() 是指坡面的铅直高度与水平宽度的比),求楼房
是指坡面的铅直高度与水平宽度的比),求楼房![]() 高度.(结果精确到0.1米)(参考数据:
高度.(结果精确到0.1米)(参考数据:![]() ,
,![]() )
)
【答案】楼房AB高度约为20.7米.
【解析】
过D作DG⊥BC于G,DH⊥AB于H,交AE于F,作FP⊥BC于P,则DG=FP=BH,DF=GP,求出∠DCG=30°,得出FP=DG=![]() CD=4.CG=
CD=4.CG=![]() DG=4
DG=4![]() ,求出DF=GP=4
,求出DF=GP=4![]() +10,证出∠DAF=30°=∠ADF,得出AF=DF=4
+10,证出∠DAF=30°=∠ADF,得出AF=DF=4![]() +10,得出FH=
+10,得出FH=![]() AF=10v5=1055.因此AH=V3FH=10+5V5,即可得出答案。
AF=10v5=1055.因此AH=V3FH=10+5V5,即可得出答案。
解:如图所示:过D作DG⊥BC于G,DH⊥AB于H,交AE于F,作FP⊥BC于P,则DG=FP=BH,DF=GP,
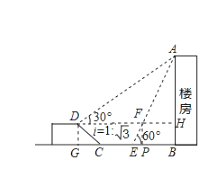
∵坡面CD=8米,山坡的坡度i=1:![]()
∴∠DCG=30°,
∴FP=DG=BH=![]() CD=4,
CD=4,
∴CG=![]() DG=4
DG=4![]() ,
,
∵∠FEP=60°,
∴FP=![]() EP=4,
EP=4,
∴EP=![]()
∴DF=GP=4![]() +10+
+10+![]() =
=![]() +10
+10
∵∠AEB=60°,
∴∠EAB=30°,
∵∠ADH=30°,
∴∠DAH=60°,
∴∠DAF=30°=∠ADF,
∴AF=DF=![]() +10.
+10.
∴FH=![]() AF=
AF=![]() +5.
+5.
∴AH=![]() FH=8+5
FH=8+5![]() .
.
∴4B=AH+BH=8+5![]() +4≈20.7(米)
+4≈20.7(米)
答:楼房AB高度约为20.7米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 上依次有
上依次有![]() 三点,
三点,![]() 的延长线交
的延长线交![]() 于
于![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() 连
连![]() 交
交![]() 于点
于点![]() .
.
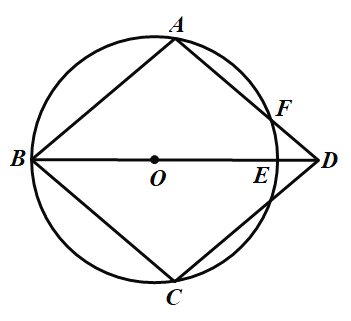
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]()
![]() 当
当![]()
![]() 时,点
时,点![]() 为弧
为弧![]() 的中点;
的中点;
![]() 若
若![]() 且
且![]() ,则
,则![]() 的半径是 .
的半径是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550年-1617年),纳皮尔发明对数是在指数概念建立之前,直到18世纪瑞士数学家欧拉(Euler,1707年-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .我们根据对数的定义可得到对数的一个性质:
.我们根据对数的定义可得到对数的一个性质:![]()
![]() .理由如下:设
.理由如下:设![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,由对数的定义得
,由对数的定义得![]() ,又因为
,又因为![]() ,所以
,所以![]() .解决以下问题:
.解决以下问题:
(1)将指数![]() 转化为对数式: .
转化为对数式: .
(2)仿照上面的材料,试证明:![]()
(3)拓展运用:计算![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
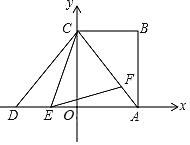
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
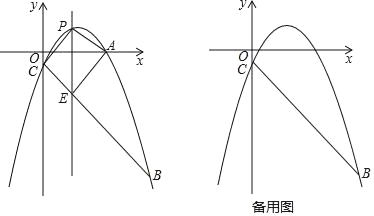
【题目】如图,已知抛物线y=﹣![]() x2+bx+c经过点A(5,
x2+bx+c经过点A(5,![]() )、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
)、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
(1)求抛物线对应的函数解析式;
(2)过点P且与y轴平行的直线l与直线BC交于点E,当四边形AECP的面积最大时,求点P的坐标;
(3)当∠PCB=90°时,作∠PCB的角平分线,交抛物线于点F.
①求点P和点F的坐标;
②在直线CF上是否存在点Q,使得以F、P、Q为顶点的三角形与△BCF相似,若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是七年级二班参加社团活动人数的扇形统计图(每位同学只参加其中一个社团).根据统计图提供的信息,下列结论正确的是( )
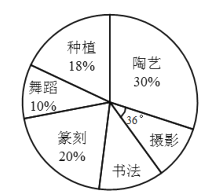
A. 参加摄影社的人数占总人数的![]()
B. 参加篆刻社的扇形的圆心角度数是![]()
C. 参加种植社的同学比参加舞蹈社的多![]() 人
人
D. 若参加书法社的人数是![]() 人,则该班有
人,则该班有![]() 人
人
查看答案和解析>>
科目:初中数学 来源: 题型:
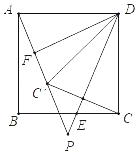
【题目】如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;
(3)连接AC,若正方形的边长为![]() ,请直接写出△ACC′的面积最大值.
,请直接写出△ACC′的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”;
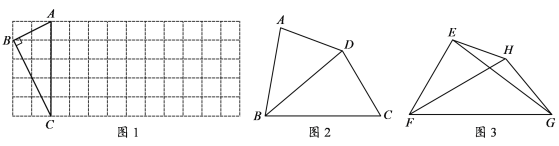
理解:
⑴ 如图1,△ABC的三个顶点均在正方形网格中的格点上,若四边形ABCD是以AC为“相似对角线”的四边形,请用无刻度的直尺在网格中画出点D(保留画图痕迹,找出3个即可);
⑵ 如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC. 请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
运用:
⑶ 如图3,已知FH是四边形EFGH的“相似对角线”, ∠EFH=∠HFG=30°.连接EG,若△EFG的面积为![]() ,求FH 的长.
,求FH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AB=4,点C是AB延长线上一点,且BC=2,点D是半圆的中点,点P是⊙O上任意一点.
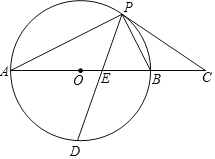
(1)当PD与AB交于点E且PC=CE时,求证:PC与⊙O相切;
(2)在(1)的条件下,求PC的长;
(3)点P是⊙O上动点,当PD+PC的值最小时,求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com