
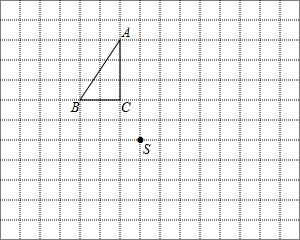 △ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.
△ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.分析 (1)△ABC绕点S按顺时针方向旋转90°得到△A1B1C1,由旋转的性质可得AB=A1B1,BC=B1C1,AC=A1C1,SC⊥SC1,SB⊥SB1,SA⊥SA1,可画出旋转后的△A1B1C1;
(2)由弧长的公式即可求出;
(3)由勾股定理求出AS=$\sqrt{{5}^{2}{+1}^{2}}$=$\sqrt{26}$,CS=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$,然后根据面积计算公式即可得出结果.
解答  解:(1)∵△ABC绕点S按顺时针方向旋转90°得到△A1B1C1
解:(1)∵△ABC绕点S按顺时针方向旋转90°得到△A1B1C1
∴AB=A1B1,BC=B1C1,AC=A1C1,SC⊥SC1,SB⊥SB1,SA⊥SA1,
故可画出旋转后的△A2B2C2,如图所示;
(2)∵BS=$\sqrt{{3}^{2}{+2}^{2}}$=$\sqrt{13}$,
∴弧BC的长=$\frac{90•π•\sqrt{13}}{180}$=$\frac{\sqrt{13}π}{2}$,
(3)∵AS=$\sqrt{{5}^{2}{+1}^{2}}$=$\sqrt{26}$,CS=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$,
∴△ABC扫过面积=S△ABC${+S}_{扇形A{SA}_{1}}$${-S}_{扇形C{SC}_{1}}$=$\frac{1}{2}×3×2$$+\frac{90•{π(\sqrt{26})}^{2}}{360}$-$\frac{90•π{•(\sqrt{5})}^{2}}{360}$=3+$\frac{21}{4}$π.
点评 本题考查了图形的变换-旋转,弧长、三角形的面积、扇形的面积的计算方法,熟记面积计算公式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
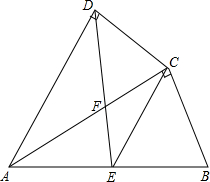 如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△BAC中,∠A=90°,∠B=60°,作AD⊥BC,垂足为D,E为边AB上一点,联结CE交AD于点P,点F为线段CE上一点,且CF:EF=3:1,联结FD.
如图,在△BAC中,∠A=90°,∠B=60°,作AD⊥BC,垂足为D,E为边AB上一点,联结CE交AD于点P,点F为线段CE上一点,且CF:EF=3:1,联结FD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com