
【题目】数学活动:拼图中的数学 数学活动课上,老师提出如下问题:
用5个边长为1的小正方形组合一个图形(相互之间不能重叠),然后将组合后的图形剪拼成一个大的正方形.
合作交流:“实践”小组:我们组合成的图形如图(1)所示,剪拼成大的正形的过程如图(2),图(3)所示.“兴趣”小组:我们组合成的图形如图(4)所示,但我们未能将其剪拼成大的正方形.
任务:请你帮助“兴趣”小组的同学,在图(4)中画出剪拼线,在图(5)中画出剪拼后的正方形.要求:剪拼线用虚线表示,剪拼后的大正方形用实线表示.
应用迁移:如图(6),∠A=∠B=∠C=∠D=∠F=90°,AB=AF=2,EF=ED=1.
请你将该图进行分割,使得分割后的各部分恰好能拼成一个正方形,请你在图(5)中画出拼图示意图(拼图的各部分不能互相重叠,不能留有空隙,不要求进行说理或证明)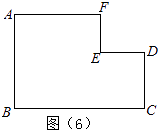
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题: 有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.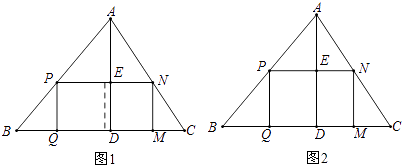
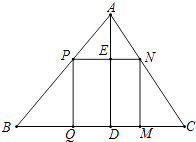
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=5,tanA= ![]() ,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E;
,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E; 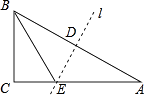
(1)求△ABC的面积;
(2)求sin∠CBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题: 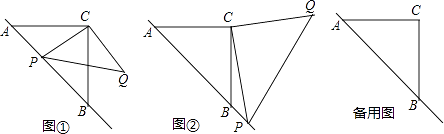
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则: ①线段PB= , PC=;
,则: ①线段PB= , PC=;
②猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE. 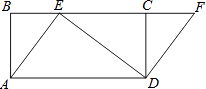
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AB的长等于;
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com