解：（1）作图正确（5分）
（2）证明：在△ACF和△AEF中
∵AE=AB=AC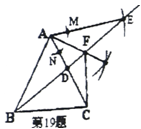 
∠EAF=∠CAF
AF=AF 
∴△ACF≌△AEF
∴∠E=∠ACF
|
练习册系列答案
相关习题
科目：初中数学 来源： 题型： 倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径。下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题。 习题解答： 习题 如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由。
习题研究
④ 类比猜想 （1）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD， ∠B=∠D， 研究一个问题，常从特例入手，请同学们研究：如图（2），在菱 形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60° 时，还有EF=BE+DF吗？ （2）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180， 查看答案和解析>> 科目：初中数学 来源： 题型： 阅读下面材料：
①连接EC，证明EC是⊙B的切线； ②在BE上是否存在一点P，使PB=PC=PE=PO，若存在，求P点坐标，并写出以P为圆心，以PB为半径的⊙P的方程；若不存在，说明理由.
查看答案和解析>> 科目：初中数学 来源： 题型： 如图，AB是半圆O的直径，D，E是半圆上任意两点，连结AD，DE，AE与BD相交于点C，要使△ADC与△ABD相似，可以添加一个条件．下列添加的条件其中错误的是( ) A．∠ACD＝∠DAB B．AD＝DE C．AD2＝BD·CD D．AD·AB＝AC·BD
查看答案和解析>> 科目：初中数学 来源： 题型： 我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务． (1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式； (2)求售价x的范围； (3)当售价x(元/台)定为多少时，商场每月销售这种空气净化器所获得的利润w(元)最大？最大利润是多少？ 查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |
观察分析 观察图（1），由解答可知，该题有用的条件是①ABCD是四边形，点E、F分别在边BC、CD上；②AB=AD；③∠B=∠D=90°；
。答：成立。
中，
，有一个锐角为60°，BC=6，若P在直线AC上（不与点A，C重合）,且
,则CP的长为_______
结果正确的是
，半径为
的圆的方程可以写为：
.
，半径为5的圆的方程为：
.
为圆心， 1为半径的圆的方程为： 
为圆心， 
为半径的圆的方程为： ；
为圆心的圆与
轴相切于原点，C是⊙B上一点，连接OC，作BD⊥OC垂足为D，延长BD交
.
的解是