
 如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$.
如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$. 分析 根据菱形的性质得出△DAB是等边三角形,进而利用全等三角形的判定得出△ABG≌△DBH,得出四边形GBHD的面积等于△ABD的面积,进而求出即可.
解答 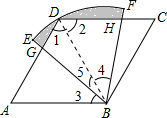 解:连接BD,
解:连接BD,
∵四边形ABCD是菱形,∠A=60°,
∴∠ADC=120°,
∴∠1=∠2=60°,
∴△DAB是等边三角形,
∵AB=6,
∴△ABD的高为3$\sqrt{3}$,
∵扇形BEF的半径为6,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AD、BE相交于点G,设BF、DC相交于点H,
在△ABG和△DBH中,$\left\{\begin{array}{l}{∠A=∠2}\\{AB=BD}\\{∠3=∠4}\end{array}\right.$,
∴△ABG≌△DBH(ASA),
∴四边形GBHD的面积等于△ABD的面积,
∴图中阴影部分的面积是:S扇形EBF-S△ABD=$\frac{60π×{6}^{2}}{360}$-$\frac{1}{2}$×6×3$\sqrt{3}$=6π-9$\sqrt{3}$.
故答案为:6π-9$\sqrt{3}$.
点评 此题主要考查了扇形的面积计算以及全等三角形的判定与性质等知识,根据已知得出四边形EBFD的面积等于△ABD的面积是解题关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a是负数 | |
| B. | 两个相似图形是位似图形 | |
| C. | 随机抛掷一枚质地均匀的硬币,落地后正面朝上 | |
| D. | 平移后的图形与原来对应线段相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
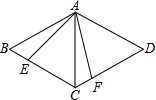 如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F.
如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y1=-(x+1)2+4.
已知抛物线y1=-(x+1)2+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
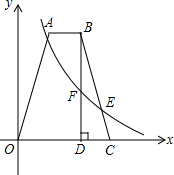 如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.
如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com