
【题目】已知等腰三角形的一边等于4cm,一边等于9cm,那么它的周长等于_____cm;若等腰三角形的一个角为70°,则它的另两个角是_____.
【答案】22, 70°,40°或55°,55°.
【解析】
分为两种情况①三角形三边为4cm,4cm,9cm,②三角形三边为4cm,9cm,9cm,看是否符合三角形的三边关系定理,求出即可;分为两种情况:①当底角为70°时,②当顶角为70°时,根据三角形的内角和定理求出即可.
解:∵等腰三角形的一边等于4cm,一边等于9cm,
∴分为两种情况:①三角形三边为4cm,4cm,9cm,
∵4+4<9,
∴不符合三角形的三边关系定理,此种情况不存在;
②三角形三边为4cm,9cm,9cm,此时符合三角形的三边关系定理,三角形的周长为4+9+9=22(cm);
∵等腰三角形的一个角为70°,
∴分为两种情况:①当底角为70°时,顶角为180°﹣70°﹣70°=40°;
②当顶角为70°时,底角为![]() ×(180°﹣70°)=55°;
×(180°﹣70°)=55°;
即它的另两个角是70°,40°或55°,55°,
故答案为:22;70°,40°或55°,55°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标和点
的横坐标和点![]() 的纵坐标都是
的纵坐标都是![]() ,求:
,求:

![]() 一次函数的解析式;(2)
一次函数的解析式;(2)![]() 的面积.
的面积.
![]() 根据图象回答:当
根据图象回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值.
为何值时,一次函数的函数值大于反比例函数的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
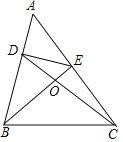
【题目】(1)如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且∠DCB=∠EBC=![]() ∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
(2)已知四边形ABCD,连接AC、BD交于O,且满足条件:AB+CD=AD+BC,AB2+AD2=BC2+DC2,请探究AC与BD的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
七年级 | a | 85 | b | S七年级2 |
八年级 | 85 | c | 100 | 160 |
(1)根据图示填空:a= ,b= ,c= ;
(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?
(3)计算七年级代表队决赛成绩的方差S七年级2,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“面积法”是指利用图形面积间的等量关系寻求线段间等量关系的一种方法.例如:在△ABC中,AB=AC,点P是BC所在直线上一个动点,过P点作PD⊥AB、PE⊥AC,垂足分别为D、E,BF为腰AC上的高.如图①,当点P在边BC上时,我们可得如下推理:
∵S△ABC=S△ABP+S△ACP
∴![]() ACBF=
ACBF=![]() ABPD+
ABPD+![]() ACPE
ACPE
∵AB=AC
∴![]() ACBF=
ACBF=![]() AC(PD+PE)
AC(PD+PE)
∴BF=PD+PE

(1)(变式)如图②,在上例的条件下,当点P运动到BC的延长线上时,试探究BF、PD、PE之间的关系,并说明理由.
(2)(迁移)如图③,点P是等边△ABC内部一点,作PD⊥AB、PE⊥BC、PF⊥AC,垂足分别为D、E、F,若PD=1,PE=2,PF=4.求△ABC的边长.
(3)(拓展)若点P是等边△ABC所在平面内一点,且点P到三边所在直线的距离分别为2、3、6.请直接写出等边△ABC的高的所有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com