
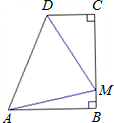
 如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则
如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则| CD |
| AB |
| x |
| y |
| 2x |
| y |
| CD |
| AB |
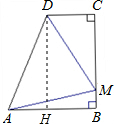 解:过点D作DH⊥AB于H,
解:过点D作DH⊥AB于H,| x |
| y |
| 2x |
| y |
| x |
| y |
| 3 |
| x |
| y |
| 3 |
| CD |
| AB |
| 3 |
| x |
| y |
| 2x |
| y |


科目:初中数学 来源: 题型:
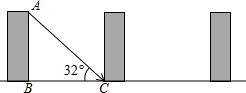 为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.
为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.| 53 |
| 100 |
| 106 |
| 125 |
| 5 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
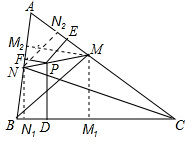 为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.
为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
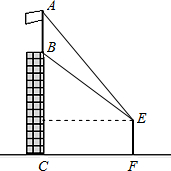 如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为60°,底部B的仰角为45°,小明的观测点E与地面的距离EF为1.6m.
如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为60°,底部B的仰角为45°,小明的观测点E与地面的距离EF为1.6m.| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
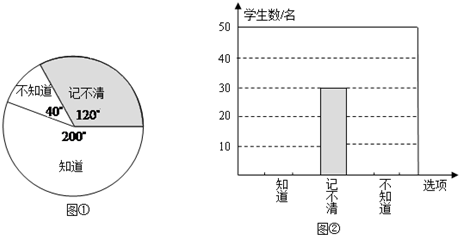
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com