
分析 当k=0,方程式一元一次方程,有实数根;根据一元二次方程的定义得k≠0,再计算判别式得到△=(3k-1)2-4k×2(k-1)=(k-1)2,然后根据非负数的性质即k的取值得到△≥0,则可根据判别式的意义得到结论.
解答 证明:当k=0,方程式一元一次方程,有实数根;
当k≠0时,
△=(3k-1)2-4k×2(k-1)=(k-1)2≥0,
方程有实数根.
综上所知,无论k取何值时kx2-(3k-1)x+2(k-1)=0恒有实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD中,AB=30,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G.连接AG、CF.下列结论:①△ABG≌△AFG;②BG=15;③△CFG是正三角形;④△FGC的面积为90.其中正确的是①②④(填所有正确答案的序号).
如图,正方形ABCD中,AB=30,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G.连接AG、CF.下列结论:①△ABG≌△AFG;②BG=15;③△CFG是正三角形;④△FGC的面积为90.其中正确的是①②④(填所有正确答案的序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
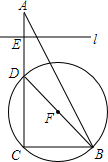 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E两点分别从顶点C、A沿着AC边向点A、C运动,点D的速度为1个单位/秒,点E的速度为2个单位/秒.以BD为直径作⊙F,过点E作CB边的平行线l,问$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E两点分别从顶点C、A沿着AC边向点A、C运动,点D的速度为1个单位/秒,点E的速度为2个单位/秒.以BD为直径作⊙F,过点E作CB边的平行线l,问$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
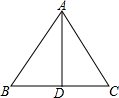 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
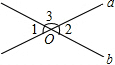 如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )
如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )| A. | 50°,40° | B. | 50°,130° | C. | 130°,50° | D. | 50°,50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 大于0.5 | B. | 等于0.5 | C. | 小于或等于0.5 | D. | 大于或等于0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com