

 ,再将A,B,
,再将A,B,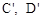 为顶点的四边形沿
为顶点的四边形沿 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形。请直接写出符合上述条件的点
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形。请直接写出符合上述条件的点 坐标,
坐标,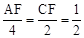 ,CF=1。
,CF=1。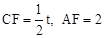 。
。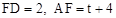 。
。 ,整理得
,整理得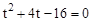 。
。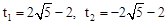 (舍去)。
(舍去)。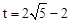 时,点C落在线段CD上。
时,点C落在线段CD上。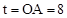 。
。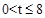 时,
时,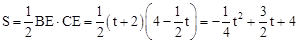 ;
;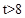 时,
时,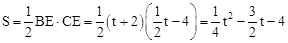 。
。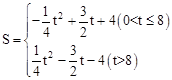 。
。 的坐标为:(12,4),(8,4),(2,4)。
的坐标为:(12,4),(8,4),(2,4)。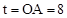 ,因此,分
,因此,分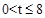 和
和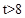 两种情况讨论。
两种情况讨论。 的坐标为:(12,4),(8,4),(2,4)。理由如下:
的坐标为:(12,4),(8,4),(2,4)。理由如下: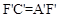 时,点
时,点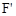 的坐标为(12,0),
的坐标为(12,0),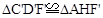 ,
,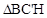 为拼成的三角形,此时点
为拼成的三角形,此时点 的坐标为(12,,4)。
的坐标为(12,,4)。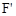 与点A重合时,点
与点A重合时,点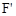 的坐标为(8,0),
的坐标为(8,0),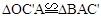 ,
,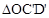 为拼成的三角形,此时点
为拼成的三角形,此时点 的坐标为(8,,4)。
的坐标为(8,,4)。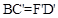 时,点
时,点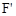 的坐标为(2,0),
的坐标为(2,0),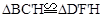 ,
,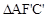 为拼成的三角形,此时点
为拼成的三角形,此时点 的坐标为(2,,4)。
的坐标为(2,,4)。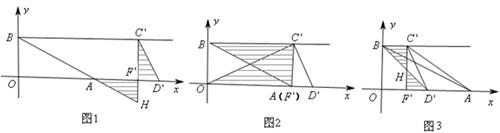


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:不详 题型:单选题

| A.轴对称图形 |
| B.中心对称图形 |
| C.既是轴对称图形又是中心对称图形 |
| D.既不是轴对称图形又不是中心对称图形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.(-1,3)和(1,-3) | B.(3,-5)和(-3,-5) |
| C.(-2,4)和(2,-4) | D.(5,-3)和(5,3) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
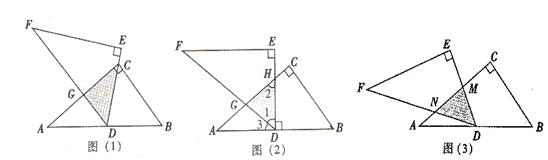
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com