
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊAЃЈЉ1ЃЌ0ЃЉЁЂCЃЈ4ЃЌ0ЃЉЃЌBCЁЭxжсгкЕуCЃЌЧвACЃНBCЃЌХзЮяЯпyЃНx2+bx+cОЙ§AЁЂBСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕуEЪЧЯпЖЮABЩЯвЛЖЏЕуЃЈВЛгыAЁЂBжиКЯЃЉЃЌЙ§ЕуEзїxжсЕФДЙЯпЃЌНЛХзЮяЯпгкЕуFЃЌЕБЯпЖЮEFЕФГЄЖШзюДѓЪБЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїEFPЪЧвдEFЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЫљгаЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
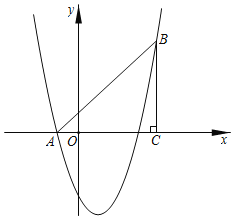
ЁОД№АИЁПЃЈ1ЃЉyЃНx2Љ2xЉ3ЃЛЃЈ2ЃЉЕуEЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉДцдкЃЌP1ЃЈ
ЃЉЃЛЃЈ3ЃЉДцдкЃЌP1ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌP2ЃЈ
ЃЉЃЌP2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌP3ЃЈ
ЃЉЃЌP3ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓЕУЕуAЕФзјБъЃЌШЛКѓНЋЕуAКЭЕуBЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНПЩЕУЕНЙигкbЁЂcЕФЗНГЬзщЃЌДгЖјПЩЧѓЕУbЁЂcЕФжЕЃЛ
ЃЈ2ЃЉЩшЕуEЕФзјБъЮЊЃЈxЃЌx+1ЃЉЃЌдђЕуFЕФзјБъЮЊFЃЈxЃЌx2Љ2xЉ3ЃЉЃЌдђПЩЕУЕНEFгыxЕФКЏЪ§ЙиЯЕЪНЃЌРћгУХфЗНЗЈПЩЧѓЕУEFЕФзюДѓжЕвдМАЕуEЕФзјБъЃЛ
ЃЈ3ЃЉДцдкЃЌЗжСНжжЧщПіПМТЧЃКЃЈiЃЉЙ§ЕуEзїaЁЭEFНЛХзЮяЯпгкЕуPЃЌЩшЕуPЃЈmЃЌm2Љ2mЉ3ЃЉЃЌгЩEЕФзнзјБъгыPзнзјБъЯрЕШСаГіЙигкmЕФЗНГЬЃЌЧѓГіЗНГЬЕФНтЕУЕНmЕФжЕЃЌШЗЖЈГіP1ЃЌP2ЕФзјБъЃЛЃЈЂЂЃЉЙ§ЕуFзїbЁЭEFНЛХзЮяЯпгкP3ЃЌЩшP3ЃЈnЃЌn2Љ2nЉ3ЃЉЃЌИљОнFЕФзнзјБъгыPЕФзнзјБъЯрЕШСаГіЙигкnЕФЗНГЬЃЌЧѓГіЗНГЬЕФНтЕУЕНnЕФжЕЃЌЧѓГіP3ЕФзјБъЃЌзлЩЯЕУЕНЫљгаТњзуЬтвтPЕУзјБъЃЎ
ЃЈ1ЃЉЁпAЃЈЉ1ЃЌ0ЃЉЁЂCЃЈ4ЃЌ0ЃЉЃЌ
ЁрOAЃН1ЃЌOCЃН4ЃЌ
ЁрACЃН5ЃЌ
ЁпBCЁЭxжсгкЕуCЃЌЧвACЃНBCЃЌ
ЁрBЃЈ4ЃЌ5ЃЉЃЌ
НЋЕуAКЭЕуBЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНЕУЃК![]() ЃЌНтЕУЃКbЃНЉ2ЃЌcЃНЉ3ЃЎ
ЃЌНтЕУЃКbЃНЉ2ЃЌcЃНЉ3ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНx2Љ2xЉ3ЃЎ
ЃЈ2ЃЉЁпжБЯпABОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ5ЃЉЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊyЃНkx+bЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊЃКyЃНx+1ЃЌ
ЁпЖўДЮКЏЪ§yЃНx2Љ2xЉ3ЃЌ
ЁрЩшЕуEЃЈtЃЌt+1ЃЉЃЌдђFЃЈtЃЌt2Љ2tЉ3ЃЉЃЌ
ЁрEFЃНЃЈt+1ЃЉЉЃЈt2Љ2tЉ3ЃЉЃНЉЃЈtЉ![]() ЃЉ
ЃЉ![]() ЃЌ
ЃЌ
ЁрЕБtЃН![]() ЪБЃЌEFЕФзюДѓжЕЮЊ
ЪБЃЌEFЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
ЁрЕуEЕФзјБъЮЊЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉДцдкЃЌЗжСНжжЧщПіПМТЧЃК
ЃЈЂЁЃЉЙ§ЕуEзїaЁЭEFНЛХзЮяЯпгкЕуPЃЌЩшЕуPЃЈmЃЌm2Љ2mЉ3ЃЉЃЌ

Ёр![]()
![]() ЃЌ
ЃЌ
Ёрm1=![]() ЃЌm2=
ЃЌm2=![]()
ЁрP1ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌP2ЃЈ
ЃЉЃЌP2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЃЈЂЂЃЉЙ§ЕуFзїbЁЭEFНЛХзЮяЯпгкP3ЃЌЩшP3ЃЈnЃЌn2Љ2nЉ3ЃЉ
дђгаЃКn2Љ2nЉ3ЃНЉ![]()
Ёрn1=![]() , n2=
, n2=![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЁрP3ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌЪЙЁїEFPЪЧвдEFЮЊжБНЧБпЕФжБНЧШ§НЧаЮЫљгаЕуPЕФзјБъЮЊЃКP1ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌP2ЃЈ
ЃЉЃЌP2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌP3ЃЈ
ЃЉЃЌP3ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
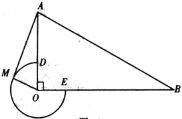
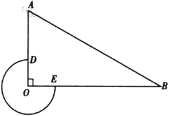
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊдВаФЃЌвд
ЮЊдВаФЃЌвд![]() ЮЊАыОЖзїгХЛЁ
ЮЊАыОЖзїгХЛЁ![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() .Еу
.Еу![]() дкгХЛЁ
дкгХЛЁ![]() ЩЯДгЕу
ЩЯДгЕу![]() ПЊЪМвЦЖЏЃЌЕНДяЕу
ПЊЪМвЦЖЏЃЌЕНДяЕу![]() ЪБЭЃжЙЃЌСЌНг
ЪБЭЃжЙЃЌСЌНг![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌХаЖЯ
ЪБЃЌХаЖЯ![]() гыгХЛЁ
гыгХЛЁ![]() ЕФЮЛжУЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЕФЮЛжУЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() дкгХЛЁ
дкгХЛЁ![]() ЩЯвЦЖЏЕФТЗЯпГЄМАЯпЖЮ
ЩЯвЦЖЏЕФТЗЯпГЄМАЯпЖЮ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ3ЃЉСЌНг![]() ЃЌЩш
ЃЌЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
БИгУЭМ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЁЂBСНЫљбЇаЃЕФбЇЩњЖМВЮМгСЫФГДЮЬхг§ВтЪдЃЌГЩМЈОљЮЊ7Љ10ЗжЃЌЧвЮЊећЪ§ЃЎССССЗжБ№ДгетСНЫљбЇаЃИїЫцЛњГщШЁвЛВПЗжбЇЩњЕФВтЪдГЩМЈЃЌЙВ200ЗнЃЌВЂЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМЃЎ
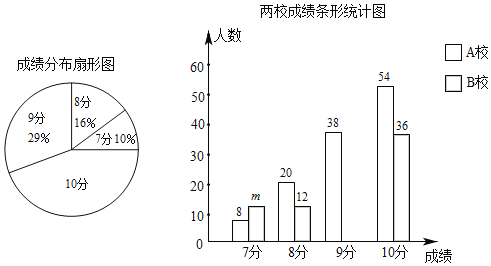
ЃЈ1ЃЉет200ЗнВтЪдГЩМЈЕФжаЮЛЪ§ЪЧЁЁ ЁЁЗжЃЌmЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛЩШаЮЭГМЦЭМжаЃЌЧѓГЩМЈЮЊ10ЗжЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ3ЃЉССССЫуГіСЫЁА1УћAаЃбЇЩњЕФГЩМЈБЛГщЕНЁБЕФИХТЪЪЧ![]() ЃЌЧыФуЙРМЦAаЃГЩМЈЮЊ8ЗжЕФбЇЩњДѓдМгаЖрЩйУћЃЎ
ЃЌЧыФуЙРМЦAаЃГЩМЈЮЊ8ЗжЕФбЇЩњДѓдМгаЖрЩйУћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
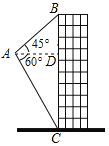
ЁОЬтФПЁПШчЭМЃЌКНХФЮоШЫЛњДгAДІВтЕУвЛДБНЈжўЮяЖЅВПBЕФбіНЧЮЊ45ЁуЃЌВтЕУЕзВПCЕФИЉНЧЮЊ60ЁуЃЌДЫЪБКНХФЮоШЫЛњгыИУНЈжўЮяЕФЫЎЦНОрРыADЮЊ110mЃЌФЧУДИУНЈжўЮяЕФИпЖШBCдМЮЊ_____mЃЈНсЙћБЃСєећЪ§ЃЌ![]() Ёж1.73ЃЉЃЎ
Ёж1.73ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАЫФъМЖЃЈ1ЃЉАрбаОПадбЇЯАаЁзщЮЊбаОПШЋаЃЭЌбЇПЮЭтдФЖСЧщПіЃЌдкШЋаЃЫцЛњбћЧыСЫВПЗжЭЌбЇВЮгыЮЪОэЕїВщЃЌЭГМЦЭЌбЇУЧвЛИідТдФЖСПЮЭтЪщЕФЪ§СПЃЌВЂЛцжЦСЫвдЯТЭГМЦЭМЃЎ
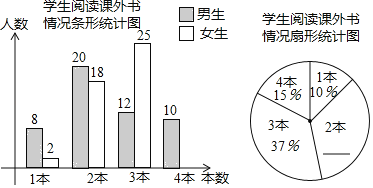
ЧыИљОнЭМжааХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЙВгаЖрЩйУћЭЌбЇВЮгыЮЪОэЕїВщЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШЋаЃЙВгабЇЩњ1500ШЫЃЌЧыЙРМЦИУаЃбЇЩњвЛИідТдФЖС2БОПЮЭтЪщЕФШЫЪ§дМЮЊЖрЩйЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪагУ1200дЊЙКНјвЛХњМзЭцОпЃЌгУ800дЊЙКНјвЛХњввЭцОпЃЌЫљЙКМзЭцОпМўЪ§ЪЧввЭцОпМўЪ§ЕФ![]() ЃЌвбжЊМзЭцОпЕФНјЛѕЕЅМлБШввЭцОпЕФНјЛѕЕЅМлЖр1дЊЃЎ
ЃЌвбжЊМзЭцОпЕФНјЛѕЕЅМлБШввЭцОпЕФНјЛѕЕЅМлЖр1дЊЃЎ
ЃЈ1ЃЉЧѓЃКМзЁЂввЭцОпЕФНјЛѕЕЅМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЭцОпЪлЭъКѓЃЌГЌЪаОіЖЈдйДЮЙКНјМзЁЂввЭцОпЃЈМзЁЂввЭцОпЕФНјЛѕЕЅМлВЛБфЃЉЃЌЙКНјввЭцОпЕФМўЪ§БШМзЭцОпМўЪ§ЕФ2БЖЖр60МўЃЌЧѓЃКИУГЌЪагУВЛГЌЙ§2100дЊзюЖрПЩвдВЩЙКМзЭцОпЖрЩйМўЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
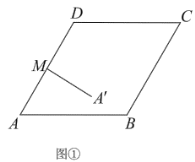
ЁОЬтФПЁПдкБпГЄЮЊ2ЕФСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() БпЕФжаЕуЃЌШєЯпЖЮ
БпЕФжаЕуЃЌШєЯпЖЮ![]() ШЦЕу
ШЦЕу![]() а§зЊЕУЯпЖЮ
а§зЊЕУЯпЖЮ![]() ЃЌ
ЃЌ
ЃЈЂёЃЉШчЭМЂйЃЌЯпЖЮ![]() ЕФГЄ__________ЃЎ
ЕФГЄ__________ЃЎ
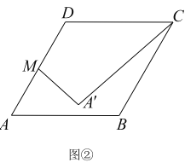
ЃЈЂђЃЉШчЭМЂкЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() ГЄЖШЕФзюаЁжЕЪЧ__________ЃЎ
ГЄЖШЕФзюаЁжЕЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ6ЗжЃЉдквЛИіВЛЭИУїЕФПкДќзАгаШ§ИіЭъШЋЯрЭЌЕФаЁЧђЃЌЗжБ№БъКХЮЊ1ЁЂ2ЁЂ3ЃЎЧѓЯТСаЪТМўЕФИХТЪЃК
ЃЈ1ЃЉДгжаШЮШЁвЛЧђЃЌаЁЧђЩЯЕФЪ§зжЮЊХМЪ§ЃЛ
ЃЈ2ЃЉДгжаШЮШЁвЛЧђЃЌМЧЯТЪ§зжзїЮЊЕуAЕФКсзјБъxЃЌАбаЁЧђЗХЛиДќжаЃЌдйДгжаШЮШЁвЛЧђМЧЯТЪ§зжзїЮЊЕуAЕФзнзјБъyЃЌЕуAЃЈxЃЌyЃЉдкКЏЪ§![]() ЕФЭМЯѓЩЯЃЎ
ЕФЭМЯѓЩЯЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛИіе§ЗНаЮжНЦЌAOBCЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЈ0ЃЌ4ЃЉЃЌЕуOЃЈ0ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ4ЃЌ4ЃЉЕуЃЎЖЏЕуEдкБпAOЩЯЃЌЕуFдкБпBCЩЯЃЌбиEFелЕўИУжНЦЌЃЌЪЙЕуOЕФЖдгІЕуMЪМжеТфдкБпACЩЯЃЈЕуMВЛгыAЃЌCжиКЯЃЉЃЌЕуBТфдкЕуNДІЃЌMNгыBCНЛгкЕуPЃЎ
ЃЈЂёЃЉШчЭМЂйЃЌЕБЁЯAEMЃН30ЁуЪБЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈЂђЃЉШчЭМЂкЃЌЕБЕуMТфдкACЕФжаЕуЪБЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈЂѓЃЉЫцзХЕуMдкACБпЩЯЮЛжУЕФБфЛЏЃЌЁїMPCЕФжмГЄЪЧЗёЗЂЩњБфЛЏЃПШчБфЛЏЃЌМђЪіРэгЩЃЛШчВЛБфЃЌжБНгаДГіЦфжЕЃЎ
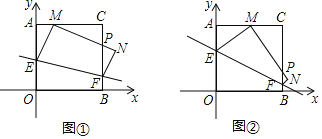
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com